「統計学関連なんでもあり」の過去ログ--- 041

No.05111　２本の直線回帰による検定について　　【くじら】　2007/12/17(Mon) 13:43

2本の直線回帰の検定について，質問させてください。
青木先生のエクセルのマクロを使わせて頂き，検討してみました。

従属変数は，有訴率です。
独立変数は，0年から50年までの年齢です。
ある年齢まで上昇し，ある年齢からは有訴率が一定の傾向が散布図から予想できたため，2本の回帰直線で検討しています。

分割点17年と18年の，「残差平方和の和 = 641」が一番低くなりました。ここに，2本の回帰直線の「分割点」すなわち，有訴率の上昇が低下する点があると考えてよろしいのでしょうか？

線を表示する時の線形近似の「予測」とは，どのような意味でしょうか？2本ともに，前方・後方ともに0単位で統一した方がよろしいですか？　青木先生のグラフでは，2本とも前方・後方ともに1単位ですが，どのような意味があるのでしょうか？

また，この結果を論文に表示するとき，R2と数式は併記すべきでしょうか？

稚拙な質問で恐縮ですが，ご教示願えればと思います。
どうぞよろしくお願いいたします。

No.05112　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/17(Mon) 14:39

> 分割点17年と18年の，「残差平方和の和 = 641」が一番低くなりました。ここに，2本の回帰直線の「分割点」すなわち，有訴率の上昇が低下する点があると考えてよろしいのでしょうか？

一応，そのように考えるのが良かろうと言うことですが，そこに真の分割点（転換点）があるかどうかは検討の余地はあるでしょう。

> 線を表示する時の線形近似の「予測」とは，どのような意味でしょうか？2本ともに，前方・後方ともに0単位で統一した方がよろしいですか？　青木先生のグラフでは，2本とも前方・後方ともに1単位ですが，どのような意味があるのでしょうか？

Excel の「近似曲線の追加」ウィンドウのことですね。
予測式（回帰直線）を描くとき，横軸の範囲をどのようにとるかということでしょう。
何単位補外しようがあなたのお好きなように(^_^;)統一する必要もないし，0にする必然性もありません。

数式は書くべきでしょう。R2も書いた方が良いとは思います。

No.05115　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/17(Mon) 15:23

お返事，どうもありがとうございます。

分割点についてですが，モデルの適合度の検討をしなければならないと考えてよろしいでしょうか？
SPSSの回帰で，重回帰として検討する

有訴の　　　　ある・なし
年齢　　　　　数値データ
ダミー変数　　分割点と思われる前後の数値を0,1データに置き換えたもの

という3変数の重回帰という方法のアドバイスを頂きましたが，それは可能でしょうか？

または，赤池のAICという指標も可能ということでしたが，回帰直線が2本のため，算出の仕方がわかりません。
ぜひ妥当性については検討したいので，お手数ですが，ご教示をお願いいたします。

No.05118　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/17(Mon) 16:15

spss についてはよくわからないので(^_^;)

http://aoki2.si.gunma-u.ac.jp/R/oresen.html
のデータ例を分析した例は添付図のようになります
用意したデータは図の右上 xg は「変換」 compute で作りました
yを従属変数，x, g, xg を独立変数として強制投入する（シンタックスは左下）と，右のような結果になりました。
先のページのRの結果と同じになります（当たり前ですが）

ちょっと気になるのは，従属変数が有訴率ということで，年齢範囲内では予測値は0～1になるのでしょうね。

AIC も，このモデルは，結局上のように，連続変数（年齢）と折れ線を示すダミー変数，および連続変数とダミー変数の交互作用項にすぎないので，普通の重回帰分析ですから，普通の場合と同じように扱えると思いますが。

図は，クリックすると原寸表示されます

No.05120　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/17(Mon) 17:00

お返事，どうもありがとうございます。疑問がどんどん解決していき，感謝です。

今，ご教示頂きましたように，解析してみました。最初のエクセルで算出した結果のR2の値が，その周辺の分割点のR2の値より一番高かったです。R2=0.85となりました。

1つ，疑問なのですが，なぜ連続変数（年齢）と，折れ線を示すダミー変数，および連続変数とダミー変数の3変数にしなければならないのでしょうか？

同様のデータを作り，解析したところ，R2=0.87とあがりましたが，連続変数とダミー変数をあわせた変数を加えて解析する意味がわかりません。

大変申し訳ありませんが，ご教授頂ければ幸いです。
どうぞよろしくお願いいたします。

No.05121　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/17(Mon) 17:37

データを分けて2本の直線にあてはめるというのと，データそのままで1つの重回帰式で表現するのが同じであるからというより説明できませんが。ようするに，交互作用も考えてはじめて完全モデルになるということです。
> a1 <- model1$coefficients[1]
> b1 <- model1$coefficients[3]
> a2 <- model1$coefficients[1]+model1$coefficients[2]
> b2 <- model1$coefficients[3]+model1$coefficients[4]
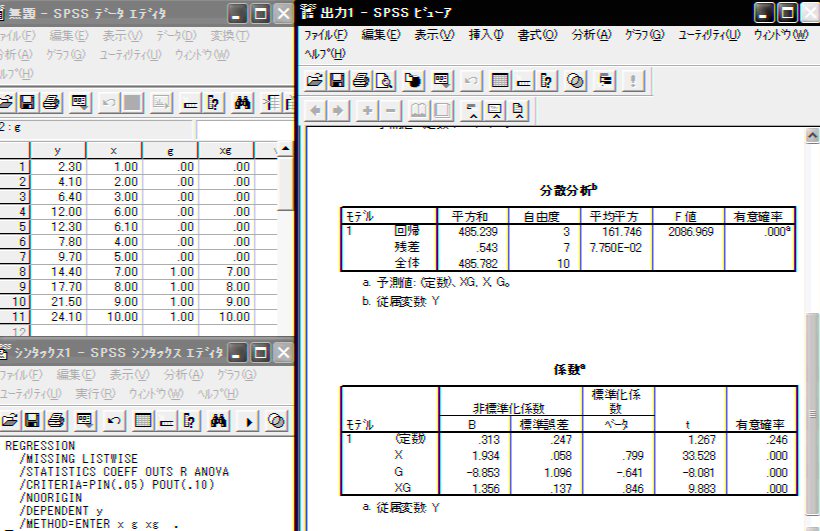
> print(sprintf("constant1 = %f,  slope1 = %f\n", a1, b1))
[1] "constant1 = 0.312848,  slope1 = 1.933951"
> print(sprintf("constant2 = %f,  slope2 = %f\n", a2, b2))
[1] "constant2 = -8.540000,  slope2 = 3.290000"
と，同じ結果になります。

No.05122　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/17(Mon) 17:55

青木先生

ご教授，どうもありがとうございました。
早速，解析をすすめてみます。
どうもありがとうございました。

No.05127　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/18(Tue) 00:29

解析をすすめて，よくわからなくなってしまったので，再度質問させてください。

直線回帰で，2本の回帰直線を引いたのですが，分割点が17と18であるにもかかわらず，2本の接点は34.6のあたりです。

分割点が 17 と 18 の間であるときが最も残差平方和が小さくなる(679.78598327183)
左側のデータについて：回帰直線の傾きは 1.05523136660114，切片は 13.2055530274923
右側のデータについて：回帰直線の傾きは 0.448257346718578，切片は 34.1978821852966
2 本の直線の交点の座標は (34.5852185928253, 49.7009605073985)

青木先生の例題のように，
分割点が 6.1 と 7 の間であるときが最も残差平方和が小さくなる(0.542521280510245)
左側のデータについて：回帰直線の傾きは 1.93395069299644，切片は 0.312848031399483
右側のデータについて：回帰直線の傾きは 3.29，切片は -8.54
2 本の直線の交点の座標は (6.52841160397146, 12.9384741770661)

私のデータでは，交点は，分割点の近辺になりません。

結果として，「このデータには分割点は17年目と18年目の間にあり，2本の直線の傾きが異なる〔有訴率の上昇の割合に違いがある〕」と考えてもよろしいのでしょうか？
このように考えると，交点の必要性は，ほぼなくなるのですが・・・。〔どこで交わっても，分割点に意味があれば，交点は問題なくなってしまうと思います。〕

また，このような直線2本は，それぞれ式とR2の値を表示するべきですよね？

このような考え方でよろしいでしょうか？
お手数をおかけ致しますが，どうぞよろしくお願いいたします。

No.05128　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/18(Tue) 10:20

> 2本の回帰直線を引いたのですが，分割点が17と18であるにもかかわらず，2本の接点は34.6のあたりです

そのようなこともあるのかなとは思います。

> このような直線2本は，それぞれ式とR2の値を表示するべきですよね？

http://aoki2.si.gunma-u.ac.jp/R/oresen.html
に示したように，一つの重回帰式として表現しても良いし，二本の回帰直線として表現しても良いでしょう。
R2 は重回帰式の結果に出ているものでよいわけです。

No.05130　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/18(Tue) 10:37

こんな風な場合ですね。
（どういう2直線を当てはめるか，単純にx座標だけで分割するのはうまくないなあ。と，再考）

No.05134　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/18(Tue) 13:37

ご教授，どうもありがとうございます。

結果のグラフを添付したかったのですが，エクセルはアップロードできないというエラーがでてしまいました。

思い違いをしていると困るので，確認させて頂きたいのですが，分割点でデータの回帰直線が2本の異なる傾きを示している(違った傾向がみられる)のではなく，交点を境として違った傾向が見られると考える方が適切でしょうか？

そもそも分割点と交点の違いは，なんでしょうか？

砂糖と水の融点のように，ある一定の量まで行くと，そのまま飽和して一定であるというデータとこのデータは異なるので，このように分割点と交点にズレが生じるのでしょうか？

思いつきで，1年目は有訴率0というデータを入れてみました。意味があるでしょうか？

なんとかグラフで発表したいのですが，苦慮しております。
大変申し訳ありませんが，ご助言を頂ければと思います。
どうぞよろしくお願いいたします。

No.05135　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/18(Tue) 16:57

閾値みたいなものがあって，それを超すと反応が異なるような場合には，横軸の値でデータを分割する方がよいのだろうけど

変化は徐々に起きるというような場合なら，交点を重視してデータを分割するかなぁ。交点の前後で分割して二本の直線を引いて，また交点を求めてということを繰り返して，データの分割点が変わらなくなったら収束とする。

とか。

このモデルは最初はホッケースティックモデルに当てはめるときに作ったもので，そのときは，データ点がそんなに多くないので，交点とデータの分割点がずれるようなことがなかったのであった。。。

No.05136　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/18(Tue) 17:51

二つの直線の交点も探索するようにしてみると以下のようになった。
テストデータは件のページのもの。
解析的に求める方が良いのだろうけど，面倒なので

> x <- c(1, 2, 3, 6, 6.1, 4, 5, 7, 8, 9, 10)
> y <- c(2.3, 4.1, 6.4, 12, 12.3, 7.8, 9.7, 14.4, 17.7, 21.5, 24.1)
> ss <- function(par)
+ {
+ 	a <- par[1] # 交点x座標
+ 	b <- par[2] # 交点y座標
+ 	c <- par[3] # 左側の直線の傾き
+ 	d <- par[4] # 右側の直線の傾き
+ 	xl <- x[x < a]
+ 	yl <- y[x < a]
+ 	yle <- c*(xl-a)+b
+ 	xr <- x[x >= a]
+ 	yr <- y[x >= a]
+ 	yre <- d*(xr-a)+b
+ 	retv <- sum((yl-yle)^2)+sum((yr-yre)^2)
+ 	return(retv)
+ }
> par <- c(mean(x), mean(y), 1, 1)
> ans <- optim(par, ss, control=list(maxit=1000))
> ans
$par
[1]  5.851518 11.335105  1.849823  3.092400

$value
[1] 0.730379

$counts
function gradient 
     287       NA 

$convergence
[1] 0

$message
NULL

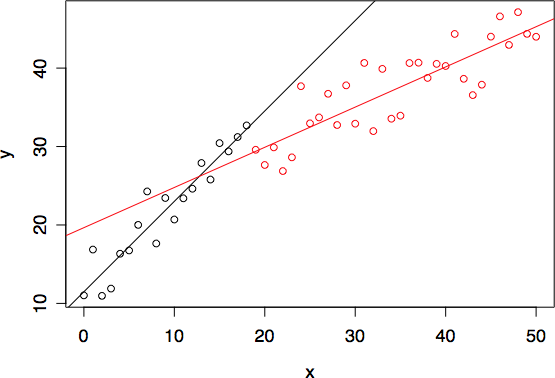
> plot(x,  y, col=ifelse(x < par[1], 3, 4))
> par <- ans$par
> a1 <- -par[3]*par[1]+par[2]
> b1 <- par[3]
> a2 <- -par[4]*par[1]+par[2]
> b2 <- par[4]
> abline(a1, b1, col=3)
> abline(a2, b2, col=4)
> cat(a1, b1) # 左側の直線の式
0.5108327 1.849823
> cat(a2, b2) # 右側の直線の式
-6.760133 3.092400

No.05139　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/18(Tue) 23:31

ご指導，どうもありがとうございます。
1日，いろいろ調べてみて，データにもミスはありませんでした。
青木先生のご助言のように，交点と分割点を，1つずつ，チェックして，交点と分割点が近似し，残差平方和の値が最小のケースを探すらしいというところまで来ました。
が，マクロでは，

分割点が 17 と 18 の間であるときが最も残差平方和が小さくなる(679.78598327183)
左側のデータについて：回帰直線の傾きは 1.05523136660114，切片は 13.2055530274923
右側のデータについて：回帰直線の傾きは 0.448257346718578，切片は 34.1978821852966
2 本の直線の交点の座標は (34.5852185928253, 49.7009605073985)

という交点の座標は，分割点でしか表示されません。
この交点の座標の位置を算出する数式は，難解なものでしょうか？

お手数をおかけし，申し訳ありません。Rもインストールしてみましたが，初心者でせっかくのプログラムが使えません。どうぞよろしくお願いいたします。

No.05140　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/18(Tue) 23:52

> という交点の座標は，分割点でしか表示されません。

どういうことでしょうか?

> この交点の座標の位置を算出する数式は，難解なものでしょうか？

別に難しくはないでしょうが，VBAプログラムを書いたりするのはプログラムできないと難しいかも知れませんね。

同じく R についても。
Rの基礎が分かれば，5136に書いたプログラムを使うのは容易なんですけどね。

No.05141　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/18(Tue) 23:59

計算してあげますから，データを書いてください

No.05142　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/19(Wed) 00:04

お返事，どうもありがとうございました。

交点の座標は，分割点でしか表示されません。
どういうことでしょうか?

分割点を 23 と 24 の間であるとしたとき
　左側の 24 個のデータについて：　　回帰直線の傾きは 1.57804325877866，切片は 8.77278146649237
　右側の 12 個のデータについて：　　回帰直線の傾きは 0.43717150359585，切片は 34.5400022821488
　残差平方和の和 = 921.894271728644

分割点として算出された以外の数値では，上記のように交点の座標までは表示されません。
今，グラフ描画のための作業領域のデータを一年ずつずらして，交点と分割点が，ほぼ一致する候補点として，22，23，24，のそれぞれの間が考えられますが，精確な交点の座標がわからず，目視で，「だいたいその辺らしい」と見当をつけました。(残差平方和もそれなりに低いです)
ただ，目視では，科学ではないので，重回帰でも検討しますが，精確な座標の位置がわかると，より明確に交点と分割点，および交差点により，精確性がわかるかと思いました。

残念ですが，VBA，R共にさわったことありません。

No.05143　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/19(Wed) 00:09

お手数をおかけして，大変申し訳ありません。
独立変数(年)	従属変数(%)
1	12.85714286
2	17.24137931
3	26.76056338
4	14.1025641
5	8.641975309
6	19.60784314
7	13.76811594
8	22.6744186
9	22.22222222
10	26.19047619
11	29
12	25.77319588
13	29.51807229
14	32.2147651
15	29.8136646
16	35.24590164
17	20.3125
18	42.68292683
19	39.16083916
20	46.26865672
21	43.78698225
22	46.11650485
23	42.12598425
24	48.40989399
25	42.79475983
26	47.5
27	45.71428571
28	48.20143885
29	41.93548387
30	50
31	44.28571429
32	46
33	51.06382979
34	58.33333333
35	45
このようなデータの時，0年の有訴率0というデータが必要か，否か，わかりません。
大変申し訳ありません。どうぞよろしくお願いいたします。

No.05146　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/19(Wed) 00:45

> 0年の有訴率0というデータが必要か，否か

不要です

> ss <- function(par)
+ {
+ 	a <- par[1] # 交点x座標
+ 	b <- par[2] # 交点y座標
+ 	c <- par[3] # 左側の直線の傾き
+ 	d <- par[4] # 右側の直線の傾き
+ 	xl <- x[x < a]
+ 	yl <- y[x < a]
+ 	yle <- c*(xl-a)+b
+ 	xr <- x[x >= a]
+ 	yr <- y[x >= a]
+ 	yre <- d*(xr-a)+b
+ 	retv <- sum((yl-yle)^2)+sum((yr-yre)^2)
+ 	return(retv)
+ }
> par <- c(mean(x), mean(y), 1, 1)
> ans <- optim(par, ss, control=list(maxit=1000))
> cat("残差平方和 =", ans$value)
残差平方和 = 829.3838
> par <- ans$par
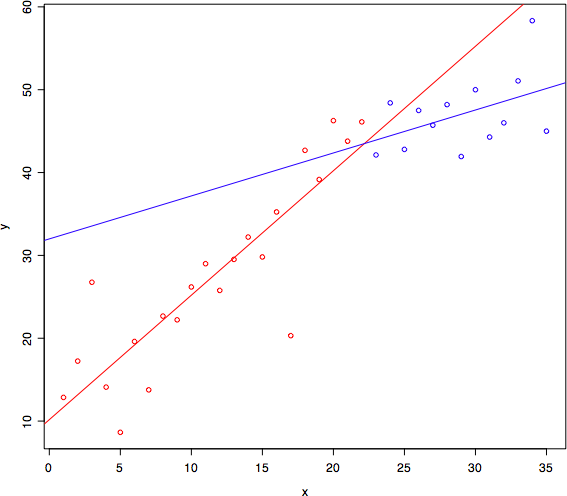
> plot(x,  y, col=ifelse(x < par[1], 2, 4))
> cat("交点座標 =", par[1], par[2])
交点座標 = 22.17134 43.4871
> a1 <- -par[3]*par[1]+par[2]
> b1 <- par[3]
> a2 <- -par[4]*par[1]+par[2]
> b2 <- par[4]
> abline(a1, b1, col=2)
> abline(a2, b2, col=4)
> cat(a1, b1) # 左側の直線の式
10.17269 1.502589
> cat(a2, b2) # 右側の直線の式
31.99127 0.5184994

画像はクリックすると原寸表示

No.05147　Re: 2本の直線回帰による検定について　　【くじら】　2007/12/19(Wed) 00:55

青木先生

どうもありがとうございました。お手数をおかけして，大変申し訳ありませんでした。
22.17の交差点と，直線の数値がわかりました。
結果をよく理解してから，仮説の検証を続けたいと思います。
どうもありがとうございました。　まずは，お礼まで。

No.05150　Re: 2本の直線回帰による検定について　　【韮澤】　2007/12/19(Wed) 12:09

横槍を入れる形で申し訳ありません。
私も折れ線による近似のプログラムを作った時に悩んだことを思い出したので，質問させて下さい。

青木先生が5130で示した様な事例があって，単純な探索では駄目なケースがあるのは知っているのですが，その様な場合の適切な解の求め方に疑問があります。

青木先生が5136/5146で示された方法は，どの様なアルゴリズムでしょうか?
(Rのプログラムを示されていますが，私がRをちゃんと勉強していないせいで，処理方法が読み取れません。申し訳ない。)
あるいは，本当は，こんな事を考えるのが良いとお考えでしたら，ヒントを教えて下さい。

ちなみに私自身は「2直線の交点が，分割点間に来ない場合は破棄」というルールで処理しました。

No.05151　Re: 2本の直線回帰による検定について　　【青木繁伸】　2007/12/19(Wed) 12:16

5136/5146 のアルゴリズムは，
　二本の直線が，点(a, b) で交わる
　左側の直線は傾きが c すなわち，y = c(x-a)+b
　右側の直線は傾きが d すなわち，y = d(x-a)+b
　a, b, c, d を探索して，合計された残差平方和が最小となるものを探索する
というものです。

No.05153　Re: 2本の直線回帰による検定について　　【韮澤】　2007/12/19(Wed) 16:18

青木先生，回答，ありがとうございました。

Rだと，optim命令で，あっさり最適探索してしまうのですね。
Windowsアプリ作らないといけない立場の私は泣けてきます。