目的

二本の直線による，折れ線回帰を行う

使用法

oresen(x, y)

print メソッド
print.oresen(obj)

plot メソッド
plot.oresen(obj, col1="red", col2="blue", ...)

引数

x	独立変数
y	従属変数
obj     oresen 関数が返すオブジェクト。クラス名は "oresen"
col1    左側のデータ点と回帰直線の描画色
col2    右側のデータ点と回帰直線の描画色
...     plot 関数，abline 関数に渡す引数

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/oresen.R", encoding="euc-jp")

# 二本の直線による，折れ線回帰を行う
oresen <- function(  x,                      # 独立変数
                        y)                      # 従属変数
{
        ss <- function(par)                  # 暫定条件下の残差平方和を求める
        {
                a <- par[1]                  # 交点の x 座標
                b <- par[2]                  # 交点の y 座標
                c <- par[3]                  # 左側の直線の傾き
                d <- par[4]                  # 右側の直線の傾き
                xl <- x[x < a]                    # データの左部分
                xr <- x[x >= a]                      # データの右部分
                if (length(xl) == 0 ||          # 左右いずれかにデータがないときには無限大を返す
                    length(xr) == 0) {
                        return(Inf)
                }
                yl <- y[x < a]
                yr <- y[x >= a]
                yle <- c*(xl-a)+b            # 左部分の予測値
                yre <- d*(xr-a)+b            # 左部分の予測値
                retv <- sum((yl-yle)^2)+
                        sum((yr-yre)^2)         # 残差平方和の和
                return(retv)
        }
        names.xy <- c(deparse(substitute(x)), deparse(substitute(y)))        # 変数名を控えておく
        OK <- complete.cases(x, y)           # 欠損値を持つケースを除く
        x <- x[OK]
        y <- y[OK]
        par <- c(mean(x), mean(y), 1, 1)     # 初期値
        ans <- optim(par, ss, control=list(maxit=1000))
        obj <- list(names.xy=names.xy, x=x, y=y, par=ans$par, residuals=ans$value)
        class(obj) <- "oresen"
        return(obj)
}
# print メソッド
print.oresen <- function(obj)
{
        cat(sprintf("残差平方和 = %g\n", obj$residuals))
        par <- obj$par
        cat(sprintf("交点座標 = ( %g, %g )\n", par[1], par[2]))
        cat(sprintf("切片 = %g, 傾き = %g\n", -par[3]*par[1]+par[2], par[3])) # 左側の回帰直線の式
        cat(sprintf("切片 = %g, 傾き = %g\n", -par[4]*par[1]+par[2], par[4])) # 右側の回帰直線の式
}
# plot メソッド
plot.oresen <- function(obj,                    # oresen オブジェクト
                        xlab=obj$names.xy[1],   # x 軸の名前
                        ylab=obj$names.xy[2],   # y 軸の名前
                        col1="red",             # 左側のデータ点と回帰直線の描画色
                        col2="blue",            # 右側のデータ点と回帰直線の描画色
                        ...)                    # plot 関数などに渡す引数
{
        par <- obj$par
        x <- obj$x
        y <- obj$y
        plot(x,  y, xlab=xlab, ylab=ylab, col=ifelse(x < par[1], col1, col2), ...)
        abline(-par[3]*par[1]+par[2], par[3], col=col1, ...)
        abline(-par[4]*par[1]+par[2], par[4], col=col2, ...)
}


使用例

> x <- c(1, 2, 3, 6, 6.1, 4, 5, 7, 8, 9, 10)
> y <- c(2.3, 4.1, 6.4, 12, 12.3, 7.8, 9.7, 14.4, 17.7, 21.5, 24.1)
> ans <- oresen(x, y)
> print(ans) # ans だけでもよい
残差平方和 = 0.730379
交点座標 = ( 5.85152, 11.3351 )
切片 = 0.510833, 傾き = 1.84982
切片 = -6.76013, 傾き = 3.0924
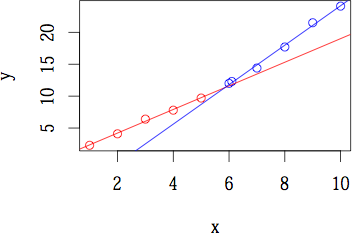
> plot(ans)