「統計学関連なんでもあり」の過去ログ--- 040

No.03936　判別分析と多重ロジスティック回帰分析などの違い　　【波音】　2007/07/18(Wed) 01:04

ある変数が0/1の2値データである場合，

1)　それを目的変数として重回帰分析を行う Rのlm()を使用
2)　それを目的変数として多重ロジスティック回帰分析を行う　Rのglm()を使用

するのとではどのような違いがあるのでしょうか。もちろん，計算過程が違うというのはあるのですが，どのようにこの2つの手法を使い分けないと"まずい"ことが生じるのですか？

それから，こういう問題を考えている際にこの掲示板の過去ログ（http://aoki2.si.gunma-u.ac.jp/lecture/mb-arc/arc010/290.html）で「2群の判別分析と重回帰分析は同じ」という記述を発見しました。これは2つの変数に回帰直線を当てはめた結果と同じになるということなのか，それとも上記1)のように2値データを目的変数として重回帰分析を行った結果と同じになるということなのかよく分かりません。

実際に，添付図のデータを自分で4通りの分析方法によって直線を当てはめてみたのですが，結局のところ，判別分析（線形判別関数による判別）とロジスティック回帰分析，2値データを目的変数とした重回帰分析の違いの区別が良く分かりません。

以前は，参考書通りに"目的にあった分析手法を選ぶ"というだけで迷うこともなかったのですが，自分で試行錯誤していたら余計に混乱してきてしまったような。。。


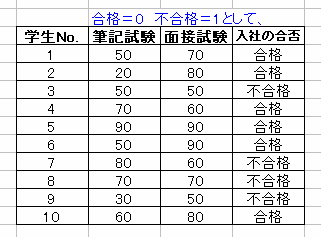
x1 <- c(50, 20, 50, 70, 90, 50, 80, 70, 30, 60)
x2 <- c(70, 80, 50, 60, 90, 90, 60, 70, 50, 80)
y <- c(0, 0, 1, 0, 0, 0, 1, 1, 1, 0)
plot(x1,x2,xlim=c(0,100), ylim=c(0,100))
#y(0/1データ)を目的変数として重回帰分析
res1 <- lm(y ~ x1 + x2)
xx <- seq(0,100,0.1)
points(xx, (2.009792+0.003550*xx)/(0.025887), type="l", col=1)
#x2を目的変数として単回帰分析
res2 <- lm(x2 ~ x1)
points(xx, 63.2304+0.1188*xx, type="l", col=2)
#判別分析をして直線を描く
my.dat <- cbind(x1, x2)
group <- matrix(y,ncol=1)
res3 <- disc(my.dat, group)
points(xx, (-11.32831941 + -0.02584958*xx)/(-0.18852368), type="l", col=3)
#多重ロジスティック回帰をして直線を描く
f.dat <- data.frame(X1 = x1, X2 = x2, Y = y)
res4 <- glm(Y ~ X1 + X2, f.dat, family = binomial)
points(xx, (10.18117+0.03019*xx)/(0.18553), type="l", col=4)

No.03938　Re: 判別分析と多重ロジスティック回帰分析などの違い　　【青木繁伸】　2007/07/18(Wed) 08:18

重回帰分析と判別分析の関係について
重回帰分析の結果で，
points(xx, (2.009792+0.003550*xx)/(0.025887), type="l", col="black",lty=2)
の定数項は，yの予測という観点から決められている
yの判別という観点からは，y=1とy=0のケースについての予測値の平均値の中点を通る直線が使われる，この直線は，傾きは同じであるが，切片は1.555513となる
> mean(x1[y==0])
[1] 56.66667
> mean(x1[y==1])
[1] 57.5
> mean(x2[y==0])
[1] 78.33333
> mean(x2[y==1])
[1] 57.5
# x1, x2 の平均値の中点での予測値を求める
> 0.00355*(56.66667+57.5)/2-0.025887*(78.33333+57.5)/2
[1] -1.555513 # この予測値をキャンセルする切片が，すなわち，1.555513
# 以下の直線が，判別分析の結果の直線と一致する
> points(xx, (1.555513+0.003550*xx)/(0.025887), type="l", col="black",lty=2)
直線回帰は意味が異なるので，対応不能。多重ロジスティック回帰は曲線回帰なので直線とは比較不能

No.03940　Re: 判別分析と多重ロジスティック回帰分析などの違い　　【波音】　2007/07/18(Wed) 11:42

回答ありがとうございます。

> yの判別という観点からは，・・・

重回帰分析で得られた結果と判別分析で得られた結果がそのまま一致するということではなかったのですね。（今回の場合に限ってたまたまそうだったのかもしれませんが）"res2 <- lm(x2 ~ x1)"の描く直線と似通っていたので，こちらと何か関係が深いのかと考えていましたがそれは関係なかったわけですね。

>　多重ロジスティック回帰は曲線回帰なので直線とは比較不能

というか，そもそも"points(xx, (10.18117+0.03019*xx)/(0.18553), type="l", col=4)"としていたのが間違いだったと認識しました。

No.03941　Re: 判別分析と多重ロジスティック回帰分析などの違い　　【青木繁伸】　2007/07/18(Wed) 12:49

> 重回帰分析で得られた結果と判別分析で得られた結果がそのまま一致するということではなかったのですね

定数項の違いだけです

判別値が正であるか負であるかで判別するために定数項を調整しているだけであって，重回帰分析の予測値の群ごとの平均値を求め，その中点の値でいずれかの群に判別するとすれば，同じことになります。
要するに，傾きは同じになります。

No.03942　Re: 判別分析と多重ロジスティック回帰分析などの違い　　【波音】　2007/07/18(Wed) 14:08

少々，面倒でも手計算（Excelを使って）で1つずつ計算して図にしてみたら，2群の平均値の中点を通るように直線の定数項（切片）を調節するということがよく理解できました。