「統計学関連なんでもあり」の過去ログ--- 039

No.01452　シグモイド曲線の比較　　【sasabe】　2006/10/27(Fri) 18:55

sasabeと申します。ホルモンの研究をしている大学院生です。
とあるホルモンの受容体をもつ培養細胞に，2種類の化学物質(A,Bとします)を別々に投与し，cAMPという物質の産生量を測定して用量反応曲線を作製しました。
EC50値が1.4倍違う(5nMと7nM)程度でグラフがほとんど重なるような結果になりました。
なんとか初めて論文の形になり雑誌に投稿したところ査読者から
「化学物質AとBの効果に違いがないとは思えない。EC50が1.4倍違うがきちんと"統計処理"すれば差があるはずである」と言われました。
今回の場合グラフ間で比較する際に有効な手法はありませんか？そもそも可能，あるいは比較が有効なのでしょうか。
曲線を直線にする方法があれば直線の傾きか何かを比較すれば良いのかとは思いましたが，
私以外に研究室で数値を扱う人がいないため，素直に言いまして困っている状態です。
長くなり申し訳ございませんが，ご回答どうぞよろしくお願い致します。

No.01453　Re: シグモイド曲線の比較　　【青木繁伸】　2006/10/27(Fri) 19:43

> EC50値が1.4倍違う(5nMと7nM)程度でグラフがほとんど重なるような結果になりました。

数式で表すと，どういう曲線なんでしょう。
EC50値が1.4倍違っても，ほとんど重なるとは?
先行研究は全くないのですか?

No.01454　Re: シグモイド曲線の比較　　【sasabe】　2006/10/27(Fri) 20:05

早速のご回答，ありがとうございます。

> 数式で表すと，どういう曲線なんでしょう。
数式はわからないのですが，グラフの例としてはhttp://www.mdf-soft.com/prism3/graph7.htmと同様です。
私もこのリンクと同じくGraphPad Prismというソフトウェアを使っています。

> EC50値が1.4倍違っても，ほとんど重なるとは?
横軸が化学物質の投与量で対数値を取ります。対数を取るためか，EC50値が1.4倍違っていても
少なくともグラフの見かけ上はほぼ同じで，ほぼ重なります。

> 先行研究は全くないのですか?
同様の実験をしてグラフやEC50値を論文に載せている論文はたくさんありますが，
投与する化学物質を変えればグラフの形やEC50値などは大きく変わるものばかりで
統計手法を使わなくても一見して明らかに違う結果であるためか，グラフ同士を比較している論文は見たことはありません。

査読者の要望に対しては，EC50の値を2物質間で単純にt検定なりで比較すれば良いだけなのかもしれませんが，
グラフの形そのものが似ているのか似ていないのか判別できるような手法があるのかと疑問に思い聞いてみた次第です。

No.01455　Re: シグモイド曲線の比較　　【sasabe】　2006/10/27(Fri) 20:22

数式がわかりました。モデル式はY=bottom+(top-bottom)/(1+10^((LogEC50-X)xHillSlope))
Xは化学物質の濃度の常用対数値で，YはcAMPの濃度です。

No.01457　Re: シグモイド曲線の比較　　【青木繁伸】　2006/10/27(Fri) 21:32

このようなグラフになるんですね?
これが「ほとんど重なるような結果」ということでしたら，検定は不要でしょう。

検定というのは，「実質的に意味のあると考えられる差が，統計学的にも意味があるといえるかどうかを知るためのもの」です。
「実質的に意味がある差ではなければ，検定など行う必要はない」のです。

参照
http://aoki2.si.gunma-u.ac.jp/lecture/Kentei/caution.html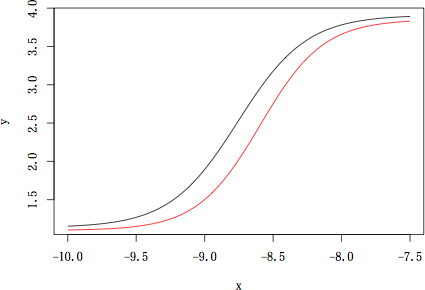

No.01458　Re: シグモイド曲線の比較　　【sasabe】　2006/10/27(Fri) 22:31

図まで作製してご説明してくださり，誠にありがとうございます。
この図の通りです。グラフのみですと差がありそうであり
各測定点から出るエラーバーを勘案すると差があるようには見えなくもなるといった状況です。この点が査読者につっこまれたのだと思います。
確かに査読者の指摘のように，違いがあってしかるべき状況なので統計処理をしてみようと思い，ここにたどり着きました。
生データもお見せすれば良かったのかもしてません公開前ですので控えさせていただきました。また上の投稿の数式も勝手ながら消させていただきました。
グラフ間で差がない，ほぼ重なっていると決めつけてしまい，思慮が足りず申し訳ございません。
再度よくよく考えてみます。ありがとうございました。

No.01459　Re: シグモイド曲線の比較　　【青木繁伸】　2006/10/27(Fri) 22:41

非線形回帰を行ったのでしょう。
LogEC50 の推定値とともに標準誤差（SE）が求められているのでは?
2つのLogEC50をa,bとし，それぞれのSEをc, d とすると，
abs(a-b)/sqrt(c^2+d^2) は近似的に標準正規分布に従うので，この値が1.96 より大きければ5%の有意水準の元でLogEC50には差があるということになるでしょう。

No.01460　Re: シグモイド曲線の比較　　【sasabe】　2006/10/27(Fri) 23:00

10例ずつの結果でご指摘の方法で計算すると0.824となりました。
ご提示の式を自分で理解した上で査読者への返答を考えたいと思います。
夜分遅くまでおつきあいくださり心より感謝致します。大変参考になりました。