No.00741 Re: 対数正規分布に従う乱数 【青木繁伸】 2006/07/27(Thu) 18:51
対数正規分布の平均値・標準偏差と,それを発生するときの正規分布の平均値・標準偏差を同じにしたいと言うことですか?
それも今までのコメントに書いてあるように,いったん作った対数正規分布の標準化をして,標準偏差倍して平均値を加えればいいのでしょ?
> n <- 10000 # 乱数の個数
> m <- 10 # 平均値
> s <- 2 # 標準偏差
# scale は,平均値0,標準偏差1に変換する関数
# rnorm は,正規乱数を発生させる関数(デフォルトでは標準正規乱数)
> x <- scale(rnorm(n))*s+m # 普通は正規化せずに rnorm(n, mean=m, sd=s)
> cat("平均値=",mean(x),"標準偏差=", sd(x))
平均値= 10 標準偏差= 2 # 指定したとおりの平均値と標準偏差になる
> lx <- scale(exp(x))*s+m # 対数正規分布に変換して,なおかつ平均値と分散を指定
> cat("平均値=",mean(lx),"標準偏差=", sd(lx))
平均値= 10 標準偏差= 2 # ちゃんとなっている
> par(mfrow=c(2,1))
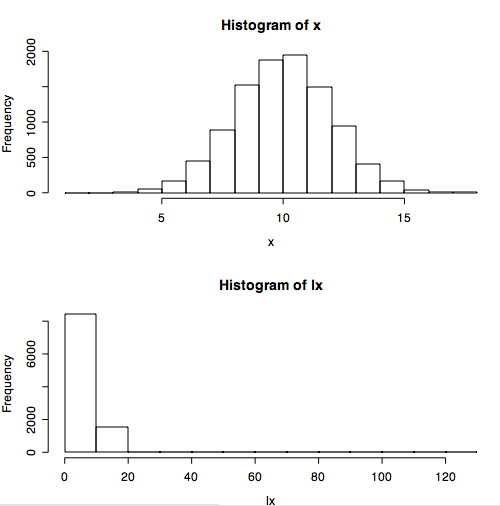
> hist(x) # ヒストグラムを描いておく
> hist(lx)