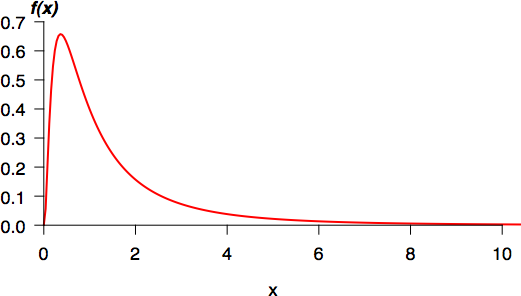
 図 1.対数正規分布の概形 |
|---|
変数 $x$ の対数をとったものが正規分布するとき,$x$ は対数正規分布に従うという。
 図 1.対数正規分布の概形 |
|---|
\[ E ( x ) = \exp \left( \mu + \frac{\sigma^{2}}{2} \right) ,\ V ( x ) = \exp ( 2 \mu + \sigma^{2} ) \left \{ \exp ( \sigma^{2} ) - 1 \right \} \] である。
図 1 の $x$ の対数をとって図を描くと,図 2 に示す標準正規分布になる。
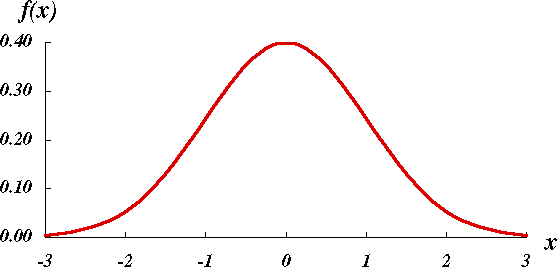 図 2.対数正規分布の横軸を対数で表すと正規分布になる |
|---|
演習問題:
応用問題: