No.00678　抗体価　　【中田】　2006/07/20(Thu) 21:14

各群の血清中の抗体価を平均値±標準偏差で表したら，平均値−標準偏差の値がマイナスになり，おかしくなりました。抗体価は平均値だけにしておいた方がよいのでしょうか。
よろしくお願い致します。
No.00680　Re: 抗体価　　【青木繁伸】　2006/07/20(Thu) 21:51

データのヒストグラムなりを描いて見ましょう。
平均値-標準偏差がマイナスの値になるということは，分布が正規分布に従っていないということを暗示していますよね。
そういうデータの平均値と算術平均値を求めて，「平均値±標準偏差」という表現をどういう意図をもってしたかと言うことですよ。
形式に従ったから？
というなら，「その形式は何を意味しているか」を理解して形式を踏襲しましたか？
単に，データがあれば【平均値と標準偏差を求めて「平均値±標準偏差」の形式表現すればよい】ということでしたら，それはやめた方が良いです。

あなたの分野（抗体価）において，データの要約値がどのように使われているかを精査するのがよいでしょう。
単に，平均値を求めて標準偏差を求めて，平均値±標準偏差という形で使われていますか。
使われていたとすると，その学会誌はちょっとうさんくさい。
抗体価の対数（たぶん2を底とする対数）の平均値（つまり，元のデータの幾何平均になりますが）を求めたりしているのではないでしょうか？よく知りませんが(^_^;)
No.00684　Re: 抗体価　　【中田】　2006/07/21(Fri) 11:37

青木先生，ご教授ありがとうございます。
各群の抗体価（2を底とする対数）を表すのに「幾何平均±標準偏差」という書き方はできるのでしょうか？
統計のことはほとんどわからず，初歩的な質問で申し訳ないのですが，抗体価の場合，幾何分布すると考えてよろしいのでしょうか。また，この分布は正規分布なのでしょうか？
よろしくお願い致します。
No.00685　Re: 抗体価　　【青木繁伸】　2006/07/21(Fri) 15:30

変数変換した後の値で求めた平均値と標準偏差を，逆変換で元の単位系に戻すときの正しいやり方については，以下を参照のこと。
http://aoki2.si.gunma-u.ac.jp/lecture/mb-arc/wrong-sd.html

> 抗体価の場合，幾何分布すると考えてよろしいのでしょうか。

さあ。それは知りませんが，抗体価って2倍2倍に薄めた液を使って反応があるかどうか見るわけだろうから，対数変換した方が解釈しやすいのではなかったかと思いますが，それこそそれは統計学が答えることと言うよりはその分野の知見が教えてくれることではないでしょうか？

> また，この分布は正規分布なのでしょうか？

どの分布ですか？対数を取った後の値の分布？
それも，ヒストグラムを描いてみると見当が付くでしょう。
データは貴方が持っているわけですから，やってみてからじゃないと何とも言えないでしょう。
No.00710　Re: 抗体価　　【中田】　2006/07/24(Mon) 11:36

青木先生，ご教授ありがとうございました。

対数正規分布に従う元のデータなら，「幾何平均±標準偏差」という表記は意味がなく，対数変換した値（対数正規分布に従う）なら，「幾何平均±標準偏差」という表記に意味があると解釈してよろしいでしょうか？

（例）サンプル：2，4，8，16，32とした場合，

(1)サンプルの幾何平均±標準偏差：8±12.20
(2)サンプルを対数変換した値の幾何平均±標準偏差：3±1.58

に なります。この場合，（1）の表記は間違いと考えてよいですよね（抗体価がマイナスになることはあり得ないわけですから）。もし，データの要約を考えれ ば，幾何平均だけを記載するのが良いのでしょうか？（2）の表記ですと，対数正規分布にしたがうわけですから，データの要約を考えれば適切な表記方法では ないかと思います。ただ，(2)のような表記をする場合，対数変換したことを明記しなければならないし，実際，「各群の幾何平均値はいくつ？」と聞かれた 場合，「8」と言いますが，「対数変換して3」とは言わないわけですから，(2）の表記方法は使用しない方が良いのではないかと考えていますが，いかがで しょうか？
よろしくお願い致します。
No.00711　Re: 抗体価　　【青木繁伸】　2006/07/24(Mon) 16:37

> 対数正規分布に従う元のデータなら，「幾何平均±標準偏差」という表記は意味がなく，対数変換した値（対数正規分布に従う）なら，「幾何平均±標準偏差」という表記に意味があると解釈してよろしいでしょうか？

ずいぶん，混乱していますね。混乱したところから結論づけは，どこが間違えているからここはこう，そこはああと言い始めたら，余計混乱するので，最初から整理しましょう。

> （例）サンプル：2，4，8，16，32とした場合，
> (1)サンプルの幾何平均±標準偏差：8±12.20
> (2)サンプルを対数変換した値の幾何平均±標準偏差：3±1.58

(1) 幾何平均は8に間違いないですが。標準偏差 12.20 とはどのように計算したものでしょうか？2,4,8,16,32 の標準偏差ですか？なぜ？

(2) 3は幾何平均ではないでしょう。データの対数(底は2として）を取ったものの平均値ですよね。3の逆対数を取ったら（2のべき乗したら，2^3）幾何平均です。

> ，（1）の表記は間違いと考えてよいですよね（抗体価がマイナスになることはあり得ないわけですから）
マイナスになるからという理由で間違いということではないです。

もう，±という表記はやめましょう。

標準偏差を示す意味をもう一度考えましょう。

2,4,8,16,32 という5個のデータがあったとして，底が2の対数を考えます。
対数を取ると，1,2,3,4,5 というデータに変換されます。
変換されたデータの平均値は 3, 標準偏差は 1.581139 です。
これを元の単位に戻すとそれが幾何平均です（3は幾何平均ではありません）
つまり 幾何平均 = 2^3 = 8
さて，変換されたデータの標準偏差を元に戻すのは何の意味もないことです
変 換されたデータの標準偏差は，変換されたデータが正規分布に従うなら，3-1.581139 〜 3+1.581139 の範囲つまり，1.418861 〜 4.581139 の範囲にデータの約68％が存在するだろうと言うことです。変換されたデータが正規分布に従わなければ，平均値と標準偏差からこのようなことを導くことは できません。

次に，元の単位で68％のデータが含まれる幾何平均を挟む二つの範囲は，2 ^ 1.418861 〜 2 ^ 4.581139 つまり 2.673744 〜 23.936475 です。「幾何平均を挟む」といったのは，幾何平均はこの範囲のど真ん中の数値ではないということです。この2つの数値を変換されたデータの平均値と標準偏 差で表せば，2^3 / 2^1.581139 と 2^3 * 2^1.581139 書き換えると 2^(3-1.581139) と 2^(3+1.581139) です。

そういう関係にあるのです。8±1.581139 でもないし 8±2^1.581139 でもありません。


なお，変換した値でも，元のままの値でも「平均値-標準偏差」の値が負になるというのは，分布が右裾が長い（対数正規分布もそのような分布の一つ）ということを表すだけです。

また，正規分布でないものは，対数正規分布だけではないので，上のような議論ができる対数正規分布は扱いやすいものなんですよね。

正規分布しないデータについて，平均値と標準偏差だけで分布の概要を要約しようと言うことに無理があるわけです。やめましょう。

ヒストグラム，箱髭図，最大値と最小値を示すなど，分布を要約する適切な方法はたくさんあります。
No.00712　Re: 抗体価　　【青木繁伸】　2006/07/24(Mon) 17:15

R でシミュレーション

底を2とする対数正規分布。対数を取ったデータでの母平均が10，母標準偏差が1のデータを1000個発生させ，x とする
x <- 2^rnorm(1000,mean=10,sd=1)

平均値，標準偏差，平均値−標準偏差を求める
> mean(x); sd(x); mean(x)-sd(x)
[1] 1328.243　平均値
[1] 1006.552　標準偏差
[1] 321.6911　平均値−標準偏差

分布がゆがんでいても，平均値−標準偏差がマイナスの値にならないこともある！！

対数正規分布（元のデータ）とその対数を取って正規分布にしたデータのヒストグラム

fig

No.00714　Re: 抗体価　　【中田】　2006/07/24(Mon) 19:36

青木先生，お忙しい中，詳細なご説明をしていただきありがとうございました。お蔭様でかなり理解することができました。しかし，まだ少し理解できないところがあります。ご教授の程，よろしくお願い致します。

＞(1) 幾何平均は8に間違いないですが。標準偏差 12.20 とはどのように計算したものでしょうか？2,4,8,16,32 の標準偏差ですか？なぜ？

標準偏差 12.20 は2,4,8,16,32 の標準偏差です。なぜ，この標準偏差の出し方が間違いなのか理解できません。

＞さて，変換されたデータの標準偏差を元に戻すのは何の意味もないことです

これは変換されたデータを元にもどすと，正規性がなくなるため，「平均値±標準偏差」の範囲に68％のデータが含まれることの意味がなくなり，これではデータの特徴を示さないことになるということでしょうか？
非正規分布においては，標準偏差という値は計算できても，それは意味のないものと考えてよろしいでしょうか？

論 文等で「平均値±標準偏差」という表記はよく見かけますので，私はデータの要約として「平均値±標準偏差」の表記をすればよいと単純に考えていました。抗 体価の平均値は，算術平均ではなく幾何平均を採り，かつ私にとって「幾何」という耳慣れない言葉を聞いたため，即，これは幾何分布するのだと思い込んでい ました。すいません，かなり勉強不足でした。

「平均値±標準偏差」という表記はデータの要約の一部として機械的に考えるのではなく，正規 分布する場合，68％のデータが含まれる範囲と考えればいいわけですね。68％のデータが含まれる範囲を表すにはどうすればよいかと考えた場合，一例とし て，データが正規分布する場合には，平均値と標準偏差で表し，非正規分布の場合には，68％のデータが含まれる範囲を表せばよいわけですね。
No.00715　Re: 抗体価　　【青木繁伸】　2006/07/24(Mon) 20:04

>> (1) 幾何平均は8に間違いないですが。標準偏差 12.20 とはどのように計算したものでしょうか？2,4,8,16,32 の標準偏差ですか？なぜ？

> 標準偏差 12.20 は2,4,8,16,32 の標準偏差です。なぜ，この標準偏差の出し方が間違いなのか理解できません。

幾 何平均は，対数変換したデータの平均値を求めてそれを元の単位に戻すために2のべき乗（対数変換の逆）を求めたのに，なんで，標準偏差は元のデータのまま の標準偏差を使うのですか？そこがおかしいのです。なぜおかしいかは，私のコメント（前のコメントも含め）書いてあります。

> 非正規分布においては，標準偏差という値は計算できても，それは意味のないものと考えてよろしいでしょうか？

標 準偏差どころか，厳密な意味で言えば，左右対象な分布でないかぎり平均値ですら意味を持ちません。平均値というと，それより大きな値を持つものと小さな値 を持つものがちょうど半々と思うでしょうが，そのような性質を持つものは平均値ではなく中央値です。平均値は分布の重心です。

なお，幾何分布という話はどこにもしていません。
例に挙げたのは対数正規分布です。対数正規分布の位置の母数の推定値としては幾何平均がふさわしいと言うだけのことです。
No.00716　Re: 抗体価　　【青木繁伸】　2006/07/24(Mon) 20:14

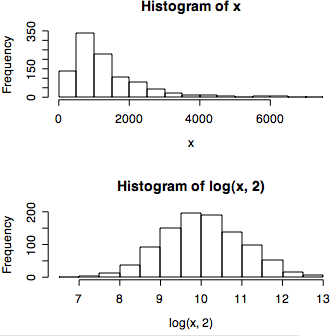
平均値と標準偏差が全く同じでも，分布はまるっきり違う

> summary <- function(x)
+ {
+ 	cat(sprintf("平均値=%.14f, 標準偏差=%.14f\n", mean(x), sd(x)))
+ 	stem(x)
+ }
> x <- scale(rnorm(40))
> y <- scale(exp(x))
> summary(x)
平均値=-0.00000000000000, 標準偏差=1.00000000000000

  The decimal point is at the |

  -3 | 5
  -2 | 4
  -1 | 530
  -0 | 9764432222210
   0 | 0122234444556788
   1 | 000369

> summary(y)
平均値=0.00000000000000, 標準偏差=1.00000000000000

  The decimal point is at the |

  -1 | 11
  -0 | 99887766655555443322110
   0 | 00012345599
   1 | 17
   2 | 6
   3 | 
   4 | 1
No.00717　Re: 抗体価　　【中田】　2006/07/24(Mon) 20:19

青木先生，度々，詳細にご回答していただきありがとうございました。
この件に関し，やっと理解できました。先生に質問する前に私なりに勉強してみたのですが，よく理解できませんでした。
お忙しいところ，このような基本的な質問に答えていただき本当に感謝しております。ありがとうございました。

● 「統計学関連なんでもあり」の過去ログ--- 039 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る