その他研究室の先生に聞いてみたのでしょうか。
実際にどの様なデータで，計算結果がどうであったかを見てもらえばいいだけでしょう。ま，その先生が正しい判断・計算をしているとしての話ですが。

現行掲示板にも同じような問題のスレッドがありましたが，変数変換を伴う場合の平均値と標準偏差の計算方法については注意が必要です。

平均値は，変数変換したデータの平均値を求めて，その値を逆変換するだけでかまいません。
しかし，標準偏差はそうではありません。
変数変換したデータの標準偏差を求めて，その値を逆変換した値は元のデータにおいて標準偏差としての意味を持たなくなります。
ここで，標準偏差の意味というのは，正規分布の場合，「平均値±1.96*標準偏差」の範囲内にデータの95%が含まれると言うことにしておきます。

例えば，「対数正規分布に従うであろう以下の10個の平均値と標準偏差を求めてください。」と言う例題を考えましょう。

50, 16, 25, 41, 11, 16, 12, 25, 13, 10

対数（自然対数としましょう）を取ったデータは
3.912023, 2.772589, 3.218876, 3.713572, 2.397895,
2.772589, 2.484907, 3.218876, 2.564949, 2.302585

平均値は 2.935886
標準偏差（不偏分散の平方根を取った方）は 0.558034

さて，この意味するところは，母集団において，「平均値±1.96標準偏差」の範囲内に95%のデータが含まれると言うことです。その限界値は 2.935886±1.96*0.558034 で，計算すると 4.029633 と 1.842139 と言うことになります。
この二つの数値を元の単位に戻すには，逆対数変換（ｅのべき乗）を施します。すなわち，exp(2.935886±1.96*0.558034) で，これは 56.240255, 6.310023 と言うことになります。 先ほど求めた平均値も，元の単位では exp(2.935886) = 18.83819 と言うことになります。 ここでの注意は，先ほどの二つの値（56.240255, 6.310023）は，平均値 18.83819 から等距離にあるのではないと言うことです。ここは，だいじなところ。対数正規分布は平均値を中心に左右対称ではないのでそれは当然のことです。

さて，間違った方法を述べましょう。
それは，先ほど求めた標準偏差の逆対数を取って元の単位に戻したと錯覚することです。
それは，exp(0.558034) = 1.747234 とすることです。平均値も逆変換して（先ほどと同じ数値） exp(2.935886) = 18.83819 ですが，平均値と標準偏差が 18.83819 と1.747234 であるとするのは間違いなのです。18.83819±1.96*1.747234 すなわち 22.27849 と 15.39788 の間にはデータの95%は含まれません。遙かに少ないデータしか含まれません。それに，この計算では二つの限界値 22.27849 と15.39788 は平均値 18.83819 から等距離にあることになってしまっています。これは，対数正規分布が非対称であることと相容れないことです。

さて，そろそろ分かってきたことですが，変数変換をしたデータから求めた標準偏差は，その段階では我々がときどき目にする「平均値±標準偏差」（より適切な書き方は「平均値は○○，標準偏差は△△」）という書き方ができるのですが，標準偏差の意味を考えて元の単位に戻した場合には，その数値はもはや我々が慣れ親しんでいる標準偏差ではない（というか，そもそもそのような数値を示すことができない）ということです。
少なくとも，変数変換したデータから計算した標準偏差を逆変換しても，それは元の単位においては何の意味もない数値であるということです。

何の意味もないというのはちょっと言い過ぎではあります。対数正規分布の場合には，以下のように考えることができます。
例えば，上で95%のデータが存在する区間の限界値は exp(2.935886±1.96*0.558034) であると書いてあります。1.96 という倍数はどうでもいいので，exp(2.935886±0.558034) を考えましょう。指数法則から，exp(2.935886)*exp(±0.558034) ですから，exp(2.935886)*exp(0.558034) と exp(2.935886)/exp(0.558034) です。exp(2.935886) = 18.83819 と exp(0.558034) = 1.747234 ですから，この数値（1.747234）は元の単位での標準偏差ではなく，これを標準偏差擬きと呼ぶとすれば，「平均値*/標準偏差擬き」ということになっているのです。

例としては，対数正規分布（対数変換）を取り上げましたが，他の変数変換でも同じです。

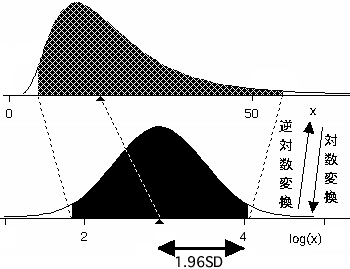
図の上側が対数正規分布に従う元のデータ。
それを対数変換すると下側の正規分布に従う。
上の横軸の各値の対数を取ったものが1対1の対応で，下側の横軸になる。
▲印は平均値。下の黒く塗った部分の上下が平均値±1.96標準偏差。
それを逆対数変換したら，上側の塗った部分の両側の値。
上側の▲は下の▲の逆対数変換だが，上の▲から塗り分けた上下に対応する値までの距離は違う。