No.00022 Re: 二次曲線近似 【青木繁伸】 06/05/12(Fri) 11:07
どうしても「紙面上で計算」しないといけないのですか？
Excel には，散布図を描いて「近似曲線をあてはめる」というのを選択すると，何次式の曲線でもあっという間に答えが出ます。「回帰分析」ツールもありますが，そ れを使うまでもないというか，「回帰分析」ツールだとデータのべき乗を前もって作成してやらないといけないので面倒です。
オンラインの解析道具もいっぱいありますが，
http://aoki2.si.gunma-u.ac.jp/JavaScript/preg.html
等はいかがでしょうか？スクリーンショットは以下のような感じ（クリックすると原寸大に拡大）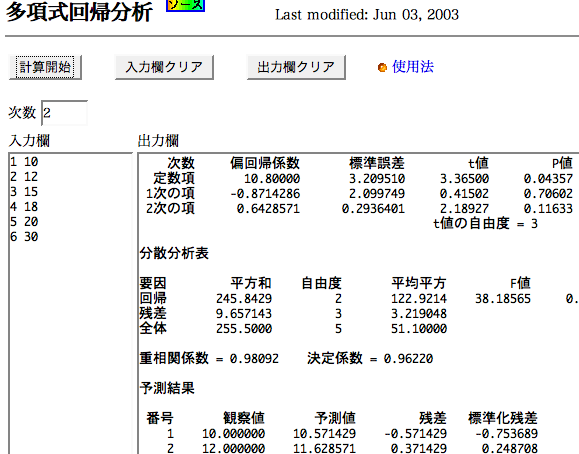
No.00024 Re: 二次曲線近似 【ms】 06/05/12(Fri) 11:15
早々とご回答ありがとうございます。
紙面上で計算したいと言った真意は解を見るより，計算過程を理解したいからです。
ツール等で確かに簡単にでる時代になりましたが，算出方法を理解せず使うのも腑に落ちないと思った為です。
引き続き，ご教授お願いいたします。
また参考になるソフトありがとうございます。
私の知っている物とは違った物なので，早速見させていただきます。
No.00027 Re: 二次曲線近似 【青木繁伸】 06/05/12(Fri) 11:59
「避けるべき解法」というのは存在すると思いますが，「特に良い解法」というのはあるのかなぁと思います。
まず，一次と二次のデータ間の相関係数行列の逆行列と，一次・二次と従属変数の相関係数ベクトルを掛けて，標準化偏回帰係数を求め，それを偏回帰係数に変換し，最後に定数項を求める。という方法ですね。
相関係数行列の代わりに変動・共変動行列から解を求めるというのでも良いのですが，演算精度によっては誤差が出たりしますので，避ける方がよい---と言うような感じ。
No.00031 Re: 二次曲線近似 【ms】 06/05/12(Fri) 14:04
回答ありがとうございます。
なるほど。ベストな解法がないとの事で，まずは青木さんに教え ていただいた解法でチャレンジしてみます。ただ，私の知識では理解できない部分が多数ありそうなので調べつつ理解していくことにします。もし，お時間ある ようでしたら，サンプルで上記解き方の式を載せていただけると大変ありがたいです。
No.00035 Re: 二次曲線近似 【青木繁伸】 06/05/12(Fri) 14:52
計算間違いがないように表形式で計算する手順を作ってみました（クリックで原寸大に拡大）。
それぞれのセルをどのように計算するか，自明なところ以外はどの箇所の数値を使って計算するのかを示しましたが，わかりにくいかも。
(1),(2),(3) はそれぞれ，x, x^2, y の値から平均値を引いたもの。
(1)^2,(2)^2 はそれぞれを二乗したもの。
(1)*(2) などは対応する列の数値を掛け合わしたもの。
予測値の欄は(-0.87143)*x + 0.642857*x^2 + 10.8
なお，計算精度を十分保つように注意のこと
また，結局，このようにして計算できても，計算方法がわかったのかどうかは疑問ですね。
そもそも，どうしてこのように計算するのかは，結局数式を示さないといけないかも知れませんし。
ということで，計算式については，
http://aoki2.si.gunma-u.ac.jp/lecture/Regression/mreg/mreg2.html
行列式，逆行列については，
http://aoki2.si.gunma-u.ac.jp/lecture/misc/sva.html
多項式回帰と重回帰の関係は，
http://aoki2.si.gunma-u.ac.jp/lecture/Regression/preg/preg.html
を参照。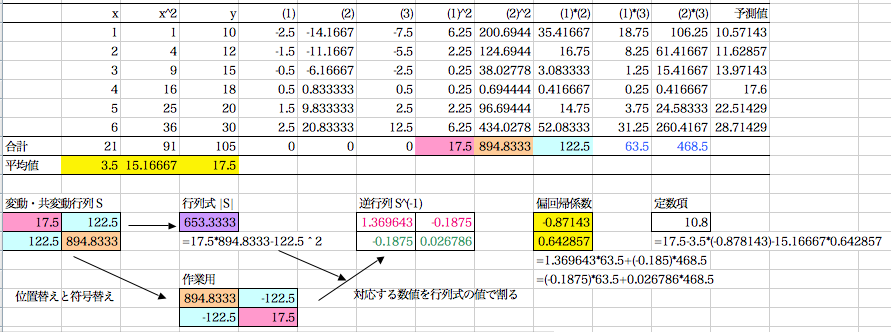
No.00036 Re: 二次曲線近似 【ms】 06/05/12(Fri) 15:08
とてもわかりやすい資料まで作っていただき，ありがとうございます。
今少しづつ式を追いながら確認しております。計算方法が納得できるようになったら
いただいたシートと照らし合わせ考えたいと思います。今後も質問させていただくかもしれませんがその時はよろしくお願いいたします。
● 「統計学関連なんでもあり」の過去ログ--- 038 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る