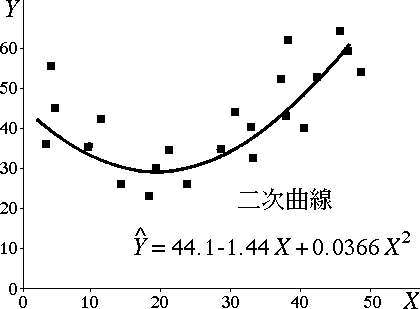
 図 1.二次式へのあてはめ例 |
|---|
多項式回帰は,重回帰分析の特別な場合である。
 図 1.二次式へのあてはめ例 |
|---|
$p$ 個の独立変数 $X_{1}, X_{2}, \dots , X_{p}$ を用いて,従属変数 $Y$ を予測する重回帰式は以下のように表される。 \[ \hat{Y} = b_0 + b_1\ X_1 + b_2\ X_2 + \dots + b_p\ X_p \] 多項式回帰では,独立変数が $1$ 個( $X$ とする )であり,$X$ の $p$ 次多項式による従属変数 $Y$ の予測式が以下のように表される。 \[ \hat{Y} = b_0 + b_1\ X + b_2\ X^2 + \dots + b_p\ X^p \] すなわち,重回帰式では $p$ 個の変数が使われるが,多項式回帰では $1$ 個の独立変数の $p$ 個のべき乗 $X^{i}\ ( i = 1, 2, \dots , p)$ が使われるという違いがある。偏回帰係数の推定法については重回帰分析を参照のこと。
次数の高い多項式を使えば,データ中の独立変数の動く範囲内ではあてはまりはよくなる。しかし,その範囲以外では全く使用に堪えない予測式ができる。次数はあまり高くしないほうがよい。
データ点が $n$ 組あるとき,$n - 1$ 次式は完全に各点を通る。$n - 1$ 次以上の多項式にはあてはめできない。なお,データ点が重なる場合には,これ以下の次数の多項式にしかあてはめできない場合もある。
演習問題:
応用問題: