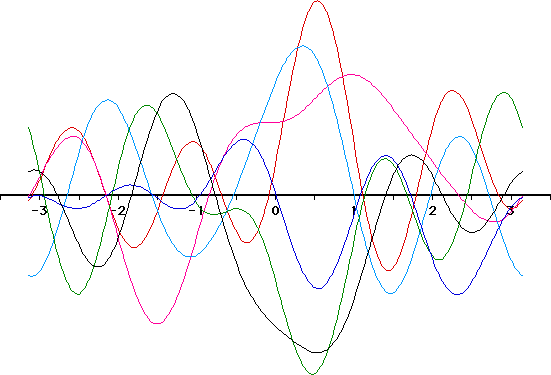
 図 1.三角多項式グラフ |
|---|
第 1 変量 $x_{1}$ に定数 $\displaystyle \frac{1}{\sqrt{2}}$,第 2 変量 $x_{2}$ に $\sin t$,第 3 変量 $x_{3}$ に $\cos t$ というように,以下順に $\sin 2t, \cos 2t, \sin 3t, \cos 3t, \sin 4t, \cos 4t,\dots$ と対応させる( $- \pi \leqq t \leqq \pi$)。これらの関数に,変量の値による重みを付けた総和を取ることによって,各対象に対応する曲線が得られる。すなわち,$i$ 番目の対象は, \[ f_i(t) = \frac{x_{1i}}{\sqrt{2}}+x_{2i}\sin t + x_{3i} \cos t + \dots \] で表される曲線として図を描く。似通った値の組を持つ対象は似通った曲線を描くことになる。
各変数は標準化しておく方が望ましい。
 図 1.三角多項式グラフ |
|---|
演習問題:
応用問題: