目的

三角多項式グラフを描く

使用法

Andrews.graph(dat, col=NULL, normalize=TRUE, points=100, main.title="Andrews' Plot")

引数

dat        多変量データ（データフレームでも行列でもよい）
col        dat の描くケースごとの色分けに使う色ベクトル。
           標準値（NULL）の場合には青色一色を使用する。
normalize  変数ごとに標準化する（標準値）。
           標準化しないときには FALSE を指定する。
points     曲線をなめらかに描くための点の数（標準値は 100）。
...        lines 屁の引数。

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/Andrews.R", encoding="euc-jp")

# 三角多項式グラフ（Andrews グラフ）
Andrews.graph <- function(   dat,                            # データ行列
                                normalize=TRUE,                 # 変数ごとに正規化する
                                points=100,                     # 曲線のなめらかさを決める
                                col=NULL,
                                ...)                            # plot への引数
{
        dat <- subset(dat, complete.cases(dat))
        dat <- as.matrix(dat)                                        # 行列に変換
        if (normalize == TRUE) {                                # normalize が TRUE なら，
                dat <- scale(dat)                            # 変数ごとに正規化する
        }
        n <- nrow(dat)                                               # 行数
        nv <- ncol(dat)                                              # 列数（変数の数）
        t <- seq(-pi, pi, length=points)                     # -π 〜 πに points 個の点を取る
        coef <- matrix(sapply(1:nv,                          # 係数行列
                function(i) if (i %% 2 == 0) sin((i%/%2)*t)
                            else cos((i%/%2)*t)),
                nrow=nv, byrow=TRUE)
        coef[1,] <- rep(1/sqrt(2), points)
        data <- matrix(sapply(1:n, function(k) colSums(dat[k,]*coef)), byrow=TRUE, nr=n)
        plot(range(t), range(data), type="n",
                xaxt="n", xlab="", ylab="")
        axis(1, at=seq(-pi, pi, length=5),
             lab=expression(-pi, -pi/2, 0, pi/2, pi))
        if (is.null(col)) {
                col <- rep("blue", n)
        }
        else if (length(col) == 1) {
                col <- rep(col, n)
        }
        invisible(sapply(1:n, function(k) lines(t, data[k,], col=col[k])))
}


使用例

data(iris)	# Fisher の iris data を図示してみる
col <- c("blueviolet", "chocolate3", "darkcyan")[as.integer(iris$Species)]		# setosa, versicolor, virginica をそれぞれ，紫，茶，緑系の色で表示する
Andrews.graph(iris[1:4], col=col, normalize=FALSE, main="iris data")  # データを標準化しない場合
Andrews.graph(iris[1:4], col=col, normalize=TRUE, main="iris data")   # データを標準化する場合

出力結果例

データを標準化しなかった場合



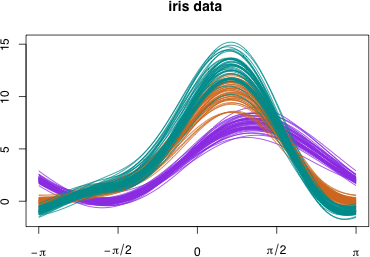データを標準化した場合



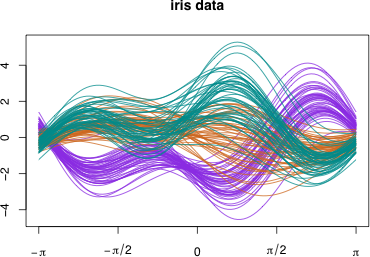
 解説ページ

 参考文献

　　河口至商，水田正弘「パソコンによる多変量グラフ解析入門」，森北出版株式会社，84〜88ページ
　　脇本和昌，後藤昌司，松原義弘著「多変量グラフ解析法」，朝倉書店，111〜113ページ
　　http://cran.r-project.org/doc/contrib/grafi3.pdf スペイン語