1. ステップワイズ変数選択によって得られた判別関数に，必要な変数が入っていない，あるいは不要な変数が入っているということが生ずる場合がある。後者の場合には最初から不要な変数を除去すればよいのであるが，前者の場合には若干の問題がある。「必要な変数」であるとした判断基準が明確ならば，判別関数を構成したい変数のセットを指定して，ステップワイズ変数選択をしないで分析する。判断基準が明確でない場合には，なぜその変数が選ばれなかったかをよく検討する必要がある。手元にあるケースが母集団を代表し得るか，他の重要な説明変数が抜けているために副作用的に選ばれなかったのではないかなど。

2. 得られた判別関数を実地へ適用する場合には，判別関数の計算が簡便になるように判別関数に含まれる変数の数が少ないことや，群の数が多い場合には各群の判別に使用する判別関数の数が少ないほうが都合がよいであろう。3 群以上の判別には正準判別分析を使用することによって，少数個の判別関数で群の判別が可能であろう。

3. 得られた判別関数は，分析に使用したケースについて最適のものであるが，別のケース群に適用しても有用であるかどうかはわからない。例えば，ある医療機関に受療した患者に適用できても，別の医療機関の受療患者には適用できないかもしれない。得られた判別関数が他の集団でも有用であるかどうか（交差妥当性を持つかどうか ）について検討したほうがよい。

4. 交差妥当性を検証するのはなかなかたいへんな場合がある。そのため，便法として折半法と呼ばれる方法がある。この方法は，既存のケースを無作為に半分ずつに分け，一方のケースを用いて判別関数を作り，もう一方のケースを得られた判別関数で判別し正判別率を検討するものである。折半法を用いるには，既存のケース数がある程度多くなければならない。

5. 判別分析は重回帰分析と密接な関連がある。二群の判別の場合，図のように従属変数を定義して重回帰分析を行うことにより，判別分析と同じ結果が得られる。

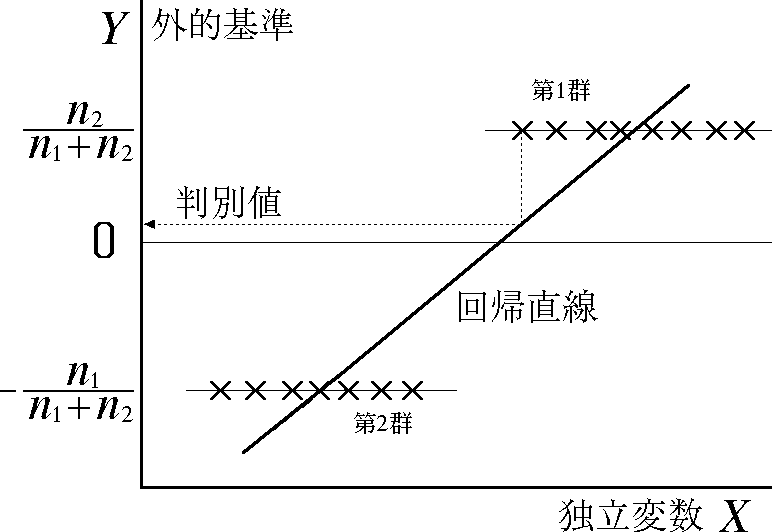   判別分析と重回帰分析の関連

演習問題：

応用問題：