例題は，二群の判別なので，答えを求める手順は若干簡単になる。
以下は実際の計算例であり，その説明は「マハラノビスの距離に基づく判別係数の求め方」の後半にある。
なお，二群の判別の場合には「相関比を最大にすることによる判別係数の求め方」によっても「同等の解」が求まる。「同等の解」というのは，全く同じ数値の解ではないが一方の解（係数と定数項の両方）が，もう一方の解の定数倍になっているということである。

> group <- rep(1:2, each=6)
> group
 [1] 1 1 1 1 1 1 2 2 2 2 2 2

> data <- data.frame(
+   X1=c(5,0,4,8,2,2,10,7,9,5,9,5),
+   X2=c(10,7,7,6,5,4,8,7,5,3,2,2))
> data
   X1 X2
1   5 10
2   0  7
3   4  7
4   8  6
5   2  5
6   2  4
7  10  8
8   7  7
9   9  5
10  5  3
11  9  2
12  5  2

> data2 <- split(data, group)
> data2
$`1`
  X1 X2
1  5 10
2  0  7
3  4  7
4  8  6
5  2  5
6  2  4

$`2`
   X1 X2
7  10  8
8   7  7
9   9  5
10  5  3
11  9  2
12  5  2

1. 各変数の平均値の差のベクトルは， \[ \mathbf{d} = ( 3.5 - 7.5, 6.5 - 4.5 ) ' = ( - 4, 2 ) ' \]

   > means <- sapply(data2, colMeans)
   > means
        1   2
   X1 3.5 7.5
   X2 6.5 4.5
   
   > d <- means[,1]-means[,2]
   > d
   X1 X2 
   -4  2 
   

2. 各群の変動・共変動行列は， \[ \mathbf{S}^{(1)} = \left( \begin{array}{rr} 39.5 & 7.5 \\ 7.5 & 21.5 \end{array} \right) \] \[ \mathbf{S}^{(2)} = \left( \begin{array}{rr} 23.5 & 14.5 \\ 14.5 & 33.5 \end{array} \right) \]

   > S <- lapply(data2, function(x) var(x)*(nrow(x)-1))
   > S
   $`1`
        X1   X2
   X1 39.5  7.5
   X2  7.5 21.5
   
   $`2`
        X1   X2
   X1 23.5 14.5
   X2 14.5 33.5
   

3. プールした分散・共分散行列 Vは，各群の変動・共変動行列の和を「全データの個数$-2$」で割ったものである。 \[ \mathbf{V} = \left( \begin{array}{rr} 6.3 & 2.2 \\ 2.2 & 5.5 \end{array} \right) \]

   > V <- (S[[1]]+S[[2]])/(nrow(data)-2)
   > V
       X1  X2
   X1 6.3 2.2
   X2 2.2 5.5
   

4. よって，解くべき連立方程式は， \[ \left \{ \begin{array}{l} 6.3\ a_1 + 2.2\ a_2 = -4 \\ 2.2\ a_1 + 5.5\ a_2 = 2 \end{array} \right . \]
5. これを解いて，$a_{1} = - 0.88561$，$a_{2} = 0.71788$ となる。

   > a <- solve(V, d)
   > a
           X1         X2 
   -0.8856089  0.7178799
   

   すなわち，判別式 $DF_0$ は，

   \[ DF_0 = -0.88561\ X_{1} + 0.71788\ X_{2} + c \] となる。

6. $c$ は任意に決めてよいが，各変数の「平均値の平均値」を判別式に代入して得られる数値の符号を変えたものにすると，$DF$ の正負で群を判別できるので便利である。

   今の場合は，平均値の平均値は，$5.5$，$5.5$ なので，$DF_0 = - 0.92251$ となり，$c = 0.92251$ とする。

   > c <- as.numeric(-a %*% rowMeans(means))
   > c
   [1] 0.9225092
   

   すなわち，最終的な判別関数は

   \[ DF = - 0.88561\ X_{1} + 0.71788\ X_{2} + 0.92251 \] となる。

7. 判別結果は表 1，図 1 のようになる。

   表 1．判別値および判別結果

   群	ケース	$X_{1}$	$X_{2}$	判別値	判別群
   1	1	5	10	3.67326	1
   1	2	0	7	5.94767	1
   1	3	4	7	2.40523	1
   1	4	8	6	$-$1.85508	2
   1	5	2	5	2.74069	1
   1	6	2	4	2.02281	1
   2	1	10	8	$-$2.19054	2
   2	2	7	7	$-$0.25159	2
   2	3	9	5	$-$3.45857	2
   2	4	5	3	$-$1.35190	2
   2	5	9	2	$-$5.61221	2
   2	6	5	2	$-$2.06978	2

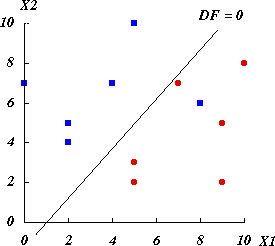   図 1．判別図

   > DF <- as.matrix(data) %*% a + c
   > DF
               [,1]
    [1,]  3.6732640
    [2,]  5.9476686
    [3,]  2.4052331
    [4,] -1.8550822
    [5,]  2.7406910
    [6,]  2.0228111
    [7,] -2.1905401
    [8,] -0.2515934
    [9,] -3.4585709
   [10,] -1.3518953
   [11,] -5.6122107
   [12,] -2.0697752
   
   > predicted <- (DF < 0)+1
   > predicted
         [,1]
    [1,]    1
    [2,]    1
    [3,]    1
    [4,]    2
    [5,]    1
    [6,]    1
    [7,]    2
    [8,]    2
    [9,]    2
   [10,]    2
   [11,]    2
   [12,]    2
   
   > plot(X2 ~ X1, data=data, col=c("blue", "red")[group], pch=c(15, 19)[group])
   > abline(-c/a[2], -a[1]/a[2])
   > text(9, 9, "DF=0")