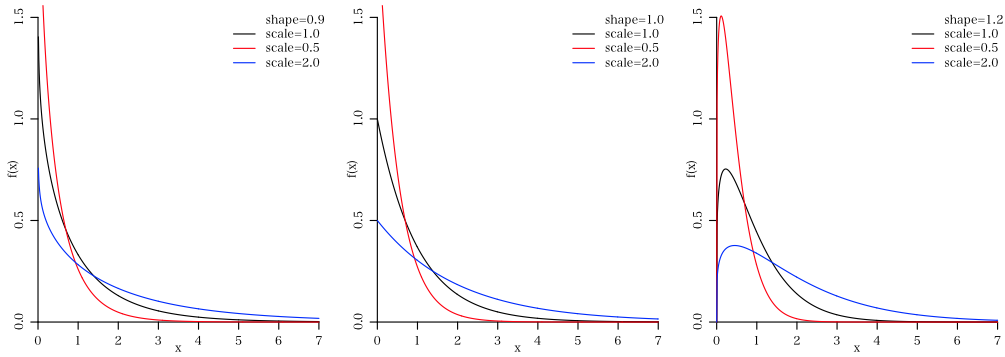
 図 1.ワイブル分布の概形 |
|---|
ワイブル分布 は機械(人間も同じ)の故障を記述する場合などにも使われる。
時点 $x$ における瞬間故障率(hazard ratio)は,ハザード関数 $\lambda(x)$ で定義される。
\[ \lambda(x)=\frac{f(x)}{1-F(x)}=\frac{m\ x^{m-1}}{\alpha} \] 時間経過に伴う瞬間故障率は,形状母数 $m$ によって変化する($\alpha$ は尺度母数)。$m \lt 1$ のときには単調減少で初期故障型,$m=1$ ならば一定で偶発故障型,$m\gt 1$ のときには単調増加で摩耗故障型となる。なお,$m=1$ の場合にはワイブル分布は指数分布に一致する。
故障の分布関数 $F(x)$ および密度関数 $f(x)$ はハザード関数から以下のように導かれる。
\[ \begin{array}{l} F(x) = 1-\exp\left (\displaystyle -\ \frac{x^m}{\alpha}\right )\\[5pt] f(x) = \displaystyle \frac{m\ x^{m-1}}{\alpha}\ \exp\left (-\ \frac{x^m}{\alpha}\right ) \end{array} \]
 図 1.ワイブル分布の概形 |
|---|
ワイブル分布の平均 $\mu$,分散 $\sigma^2$ は以下のようになる。
\[ \begin{array}{l} \mu = \alpha^{1/m}\ \Gamma \left(\displaystyle \frac{1}{m}+1 \right)\\[5pt] \sigma^2 = \alpha^{2/m} \left\{ \Gamma \left(\displaystyle \frac{2}{m}+1 \right) - \Gamma^2 \left(\displaystyle \frac{1}{m}+1 \right) \right\} \end{array} \] 注:分布関数は,上のように $F(x) = 1 - \exp \left(\displaystyle -\ \frac{x^m}{a}\right)$ と定義されるときと $F(x) = 1 - \exp\left(\displaystyle -\ \left\{ \frac{x}{b} \right)^m\right\}$ と定義されることがある(R の *weibull 関数など)。これは単純に表現上の問題であり,$m$ も $b$ も尺度パラメータと呼ばれ,両者の間には,$a = b^m$ あるいは $b = a^{1/m}$ という関係がある。どちらも同じ分布関数であるが,解析法や関数がどちらの表現を仮定しているかを確かめておかねばならない。
演習問題:
応用問題: