t 分布表　両側確率の計算　パーセント点の計算

　確率変数 $x$ の標本平均値を $\bar{x}$，標本不偏分散を $U$，母平均値を $\mu$ としたとき， \[ t = \frac{\bar{x}-\mu}{\sqrt{U\ /\ n}} \] が，自由度 $\phi = n - 1$ の $t$ 分布に従うことを，20 世紀はじめに“Student”（W. S. ゴセットのペンネーム）が報告した。 \[ f_\phi(t) = \frac{1}{\sqrt{\phi}\ B(\phi\ /\ 2, 1\ /\ 2)}\left( 1+\frac{t^2}{\phi} \right)^{-(\phi+1)\ /\ 2} \] 　$B ( \lambda_{1}， \lambda_{2} )$ はベータ関数である。

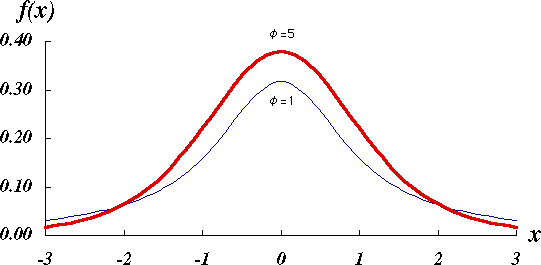図 1．$t$ 分布の概形

　自由度が $1$ のときはコーシー分布なので平均値は定義できないが，自由度が $2$ 以上のときの平均 $E ( t )$ は \[ E(t)=0 \] である。

　自由度が無限大のとき，$t$ 分布は正規分布になる。

演習問題：

応用問題：