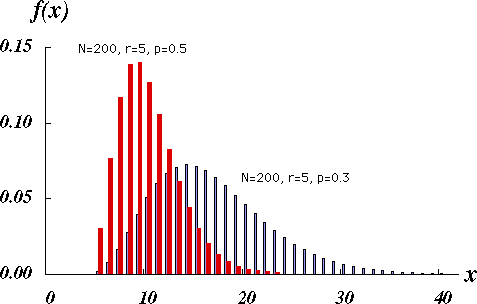
 図 1.負の超幾何分布の概形 |
|---|
大きさ $N$ の母集団で,特性 A を持つものの割合を $p$ とする。この母集団から $x$ 個目の標本を取り出したときにちょうど特性 A を持つ標本が $r$ 個になる確率を考える。
したがって,求める確率は次式で表される。 \[ f(x) = \frac{\displaystyle {N\ p \choose r-1} \times {N\ q \choose x-r}}{\displaystyle {N \choose x-1}} \times \frac{ N\ p - r + 1} {N - x + 1 } = \frac{\displaystyle {x-1 \choose r-1}\times{N-x \choose N\ p-r}} {\displaystyle {N \choose N\ p}} \]
 図 1.負の超幾何分布の概形 |
|---|
この分布は負の超幾何分布と呼ばれ,$N \rightarrow \infty$ のときには,負の二項分布に一致する。
演習問題:
応用問題: