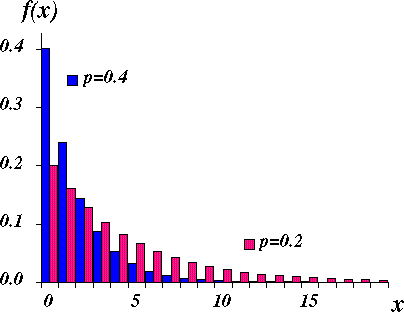
 図 1.幾何分布の概形 |
|---|
ベルヌーイ試行において,$x$ 回の失敗のあと $x+1$ 回目に初めて事象 A が起こる確率を考える。
すなわち,$x$ 回は事象 A が起こらないのでその確率は $q^x$ であり,$x+1$ 回目に事象 A が確率 $p$ で起こるので,その積が求める確率となる。
\[ f ( x ) = q^ x\ p ,\ p \gt 0,\ q \gt 0,\ p + q = 1,\ x = 0, 1, \dots \]
 図 1.幾何分布の概形 |
|---|
平均 $E ( x )$ ,分散 $V ( x )$ は
\[ E ( x ) = \frac{q}{p},\ V ( x ) = \frac{q}{p^{2}} \] である。
演習問題:
応用問題: