$F$ 分布表　上側確率の計算　パーセント点の計算

　二つの確率変数 $\chi_{1}^{2}$，$\chi_{2}^{2}$ があり，これらが互いに独立にそれぞれ自由度 $\phi_{1}$，$\phi_{2}$ の $\chi^2$ 分布に従うとき， \[ F = \frac{\chi_{1}^{2}\ \bigm /\ \phi_{1}} {\chi_{2}^{2}\ \bigm /\ \phi_{2}},\ F \geqq 0 \] も，ひとつの確率変数である。

　$0 \lt F \lt \infty$ において， 　 \[ 　 f_{\phi_1, \phi_2}(F) = \frac{\phi_1^{\phi_1/2}\ \phi_2^{\phi_2/2}}{B(\phi_1/2, \phi_2/2)}\ \frac{F^{\phi_1/2-1}}{(\phi_1F+\phi_2)^{(\phi_1+\phi_2)/2}} 　 \] は，第 1 自由度 $\phi_{1}$，第 2 自由度 $\phi_{2}$ の $F$ 分布 といわれる。

　$B ( \lambda_{1}， \lambda_{2} )$ はベータ関数である。

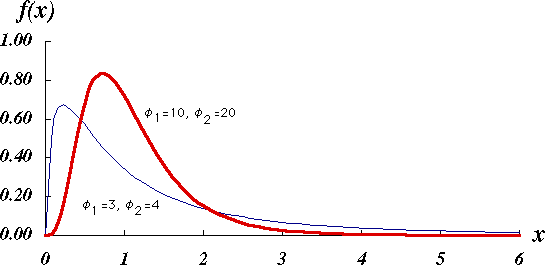図 1．$F$ 分布の概形

演習問題：

応用問題：