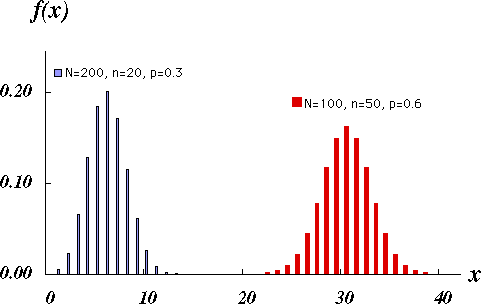
 図 1.超幾何分布の概形 |
|---|
大きさ $N$ の母集団で,特性 A を持つものの割合を $p$ とする。この母集団から $n$ 個の標本を取り出したとき,特性 A を持つ標本が $x$ 個である確率を考える。
まず,標本の選び方は ${}_{N}C_{n}$ 通り,特性 A を持つものから $x$ 個選ぶ方法は ${}_{Np}C_{x}$ 通り,そして特性 A を持たないものの選び方は ${}_{Nq}C_{n-x}$ 通りある( $p + q = 1$ )。
よって求める確率は次式で表される。 \[ f(x) = \frac{{}_{N\ p}C_{x}\times {}_{N\ q}C_{n-x}}{{}_{N}C_{n}} = \frac{\displaystyle {N\ p \choose x}\ {N\ q \choose n-x}}{\displaystyle {N \choose n}} \tag{1} \]
 図 1.超幾何分布の概形 |
|---|
この分布を超幾何分布と呼ぶ。$N$ が十分大きければ,超幾何分布は二項分布によって近似できる。
平均 $E ( x )$ ,分散 $V ( x )$ は
\[ E ( x ) = n\ p, \ V ( x ) = \frac{ n\ p\ q\ ( N - n ) }{ N - 1 } \] であり,平均は $N$ の大きさとは無関係である。
例題: 「52 枚のトランプのカードから 5 枚取り出したとき,エースがちょうど 3 枚である確率を求めよ。」
解答: ( 1 )式から, \[ p = \frac{\displaystyle {4 \choose 3}\ {48 \choose 2}}{\displaystyle {52 \choose 5}} = 0.00173608 \]
演習問題:
応用問題: