判別分析（二次の判別関数） Last modified: Aug 27, 2009
目的
二次の判別関数を使った判別分析を行う。
（R の MASS パッケージに qda, predict.qda がある）
使用法
quad.disc(data, group, func.name=c("solve", "ginv"))
print.quad.disc(obj, digits=5)
summary.quad.disc(obj, digits=5)
plot.quad.disc(obj, which=c("boxplot", "barplot", "scatterplot"), nclass=20, pch=1:obj$ngroup, col=1:obj$ngroup, xpos="topright", ypos=NULL, ...)
引数
data データ行列（行がケース，列が変数）
group 各ケースがどの群であるかを表す変数
func.name 逆行列を計算する関数名（solve か ginv）。
普通に逆行列が求まる場合にはどちらを使っても結果は同じ
省略時は solve
ムーア・ペンローズ型一般化逆行列を使うときは ginv
obj quad.disc 関数が返すオブジェクト
digits 結果の表示桁数
which 2 群判別の場合に，描画するグラフの種類
nclass barplot のときのおよその階級数
pch scatterplot を描く記号
col scatterplot の記号の色
xpos, ypos scatterplot の凡例の位置
... boxplot, barplot, scatterplot に引き渡す引数
ソース
インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/quad_disc.R", encoding="euc-jp")
# 二次の判別関数
quad.disc <- function( data, # 説明変数データ行列
group, # グループを表すベクトル
func.name=c("solve", "ginv")) # 逆行列を求める関数
{
inverse <- if (match.arg(func.name) == "solve") solve else { library(MASS); ginv}
data <- as.data.frame(data)
if (is.null(colnames(data))) {
colnames(data) <- paste("Var", 1:p, sep="")
}
vname <- colnames(data)
group <- as.factor(as.matrix(group)) # 群を表す変数は factor にする
OK <- complete.cases(data, group) # 欠損値を持つケースを除く
data <- as.matrix(data[OK,])
group <- group[OK]
p <- ncol(data) # 説明変数の個数
n <- nrow(data) # データの個数
n.i <- table(group) # 各群の例数
g.name <- names(n.i) # 群の名前
k <- length(n.i) # 群の個数
group.means <- matrix(unlist(by(data, group, colMeans)), p) # 各群・各変数の平均
vars <- array(unlist(by(data, group, var)), c(p, p, k)) # 各群の分散・共分散行列
inv.vars <- array(apply(vars, 3, inverse), c(p, p, k)) # 各群の分散・共分散行列の逆行列
scores <- sapply(1:k, function(i) { # 各ケースの各群からの距離
temp <- t(data)-group.means[,i];
sapply(1:n, function (j) temp[,j]%*%inv.vars[,,i]%*%temp[,j])
}
)
p.values <- pchisq(scores, p, lower.tail=FALSE) # 各ケースが各群に属する確率
prediction <- as.factor(g.name[apply(p.values, 1, order)[k,]]) # どの群に属するか判別
correct <- ifelse(prediction == group, TRUE, FALSE) # 判別が正しいか？
correct.table <- table(group, prediction) # 判別結果概括表
correct.rate <- sum(diag(correct.table))/n*100 # 正判別率
# add names
colnames(group.means) <- colnames(scores) <- colnames(p.values) <- dimnames(vars)[[3]] <- dimnames(inv.vars)[[3]] <- g.name
colnames(vars) <- rownames(vars) <- colnames(inv.vars) <- rownames(inv.vars) <- rownames(group.means) <- vname
rownames(scores) <- rownames(p.values) <- paste("case", 1:n)
return(structure(list(group.means=group.means, vars=vars, inv.vars=inv.vars, scores=scores, p.values=p.values, prediction=prediction, correct=correct, correct.table=correct.table, correct.rate=correct.rate, group=group, ngroup=k), class="quad.disc"))
}
# print メソッド
print.quad.disc <- function( obj, # quad.disc 関数が返すオブジェクト
digits=5) # 結果の表示桁数
{
cat("\n判別結果\n\n")
print(obj$correct.table)
cat(sprintf("\n正判別率 = %.1f %%\n", obj$correct.rate))
}
# summary メソッド # すべての結果を表示する
summary.quad.disc <- function( obj, # quad.disc が返すオブジェクト
digits=5) # 結果の表示桁数
{
print.default(obj, digits=digits)
}
# plot メソッド
plot.quad.disc <- function( obj, # quad.disc 関数が返すオブジェクトの
which=c("boxplot", "barplot", "scatterplot"), # 箱髭図か棒グラフか散布図かの選択
nclass=20, # barplot の場合のおよその階級数
pch=1:obj$ngroup, # scatterplot を描く記号
col=1:obj$ngroup, # scatterplot の記号の色
xpos="topright", ypos=NULL, # scatterplot の凡例の位置
...) # boxplot, barplot, plot に引き渡す引数
{
if (obj$ngroup == 2) {
group <- obj$group
score <- obj$score[,1]-obj$score[,2]
which <- match.arg(which)
if (which == "boxplot") { # boxplot
plot(score ~ group, xlab="群", ylab="二乗距離の差", ...)
}
else if (which == "barplot") { # barplot
tbl <- table(group, cut(score,
breaks=pretty(score, n=nclass)))
barplot(tbl, beside=TRUE, legend=TRUE, xlab="二乗距離の差", ...)
}
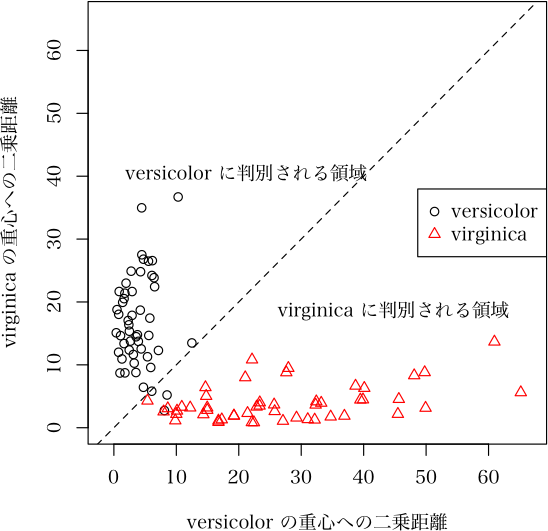
else { # scatterplot 各群の重心までの二乗距離
group <- obj$group
group.levels <- levels(group)
score1 <- obj$score[,1]
score2 <- obj$score[,2]
max1 <- max(score1)
max2 <- max(score2)
max0 <- max(max1, max2)
plot(score1, score2, col=col[as.integer(group)], pch=col[as.integer(group)],
xlim=c(0, max0), xlab=paste(group.levels[1], "の重心への二乗距離"),
ylim=c(0, max0), ylab=paste(group.levels[2], "の重心への二乗距離"), asp=1, ...)
abline(0, 1, lty=2)
text(max1, max2/2, paste(group.levels[2], "に判別される領域"), pos=2)
text(0, max2+strheight("H")*1.5, paste(group.levels[1], "に判別される領域"), pos=4)
legend(x=xpos, y=ypos, legend=group.levels, col=col, pch=pch)
}
}
else {
warning("3群以上の場合にはグラフ表示は用意されていません")
}
}
使用例
data(iris) # Fisher のアヤメのデータ
result <- quad.disc(iris[1:4], iris[5]) # quad.disc 関数からの出力は自動的には出力されないので注意
result # 結果を出力する
出力結果例
> (result <- quad.disc(iris[1:4], iris[5]) ) # print による結果出力
判別結果
prediction
group setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 3
virginica 0 0 50
正判別率 = 98.0 %
> summary(result) # summary による結果出力
$group.means # 各群ごとの平均値
setosa versicolor virginica
Sepal.Length 5.006 5.936 6.588
Sepal.Width 3.428 2.770 2.974
Petal.Length 1.462 4.260 5.552
Petal.Width 0.246 1.326 2.026
$vars # 各群の分散・共分散行列
, , setosa
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.124249 0.099216 0.0163551 0.0103306
Sepal.Width 0.099216 0.143690 0.0116980 0.0092980
Petal.Length 0.016355 0.011698 0.0301592 0.0060694
Petal.Width 0.010331 0.009298 0.0060694 0.0111061
, , versicolor
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.266433 0.085184 0.182898 0.055780
Sepal.Width 0.085184 0.098469 0.082653 0.041204
Petal.Length 0.182898 0.082653 0.220816 0.073102
Petal.Width 0.055780 0.041204 0.073102 0.039106
, , virginica
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.404343 0.093763 0.303290 0.049094
Sepal.Width 0.093763 0.104004 0.071380 0.047629
Petal.Length 0.303290 0.071380 0.304588 0.048824
Petal.Width 0.049094 0.047629 0.048824 0.075433
$inv.vars # 各群の分散・共分散行列の逆行列
, , setosa
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 18.9434 -12.4048 -4.5002 -4.7761
Sepal.Width -12.4048 15.5705 1.1111 -2.1041
Petal.Length -4.5002 1.1111 38.7762 -17.9350
Petal.Width -4.7761 -2.1041 -17.9350 106.0459
, , versicolor
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 9.5028 -3.6762 -8.6317 6.4545
Sepal.Width -3.6762 19.7110 2.1160 -19.4803
Petal.Length -8.6317 2.1160 19.8038 -26.9372
Petal.Width 6.4545 -19.4803 -26.9372 87.2448
, , virginica
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 10.5339 -3.4797 -9.9601 1.7882
Sepal.Width -3.4797 15.8754 1.1027 -8.4729
Petal.Length -9.9601 1.1027 13.4058 -2.8909
Petal.Width 1.7882 -8.4729 -2.8909 19.3141
$scores # ユークリッドの二乗距離
setosa versicolor virginica
case 1 0.44911 114.80449 182.93591
case 2 2.08109 83.31536 153.97495
case 3 1.28434 94.92043 160.49415
case 4 1.70621 82.77880 140.64139
case 5 0.76169 120.48102 184.03695
case 6 3.71265 120.48007 183.29809
【中略】
case 147 578.01838 23.36413 4.00770
case 148 618.18551 16.74095 1.11181
case 149 720.69230 33.20289 3.94189
case 150 550.78799 10.11250 2.69108
$p.values # 各群への所属の確率
setosa versicolor virginica
case 1 9.7826e-01 6.8699e-24 1.7457e-38
case 2 7.2085e-01 3.4538e-17 2.8628e-32
case 3 8.6403e-01 1.1849e-19 1.1454e-33
case 4 7.8959e-01 4.4882e-17 2.0574e-29
case 5 9.4351e-01 4.2162e-25 1.0126e-38
case 6 4.4629e-01 4.2181e-25 1.4594e-38
【中略】
case 147 8.8576e-124 1.0709e-04 4.0497e-01
case 148 1.7956e-132 2.1703e-03 8.9239e-01
case 149 1.1523e-154 1.0855e-06 4.1393e-01
case 150 6.9093e-118 3.8575e-02 6.1078e-01
$prediction # 判別結果
[1] setosa setosa setosa setosa setosa
[6] setosa setosa setosa setosa setosa
[11] setosa setosa setosa setosa setosa
[16] setosa setosa setosa setosa setosa
[21] setosa setosa setosa setosa setosa
[26] setosa setosa setosa setosa setosa
[31] setosa setosa setosa setosa setosa
[36] setosa setosa setosa setosa setosa
[41] setosa setosa setosa setosa setosa
[46] setosa setosa setosa setosa setosa
[51] versicolor versicolor versicolor versicolor versicolor
[56] versicolor versicolor versicolor versicolor versicolor
[61] versicolor versicolor versicolor versicolor versicolor
[66] versicolor versicolor versicolor versicolor versicolor
[71] virginica versicolor virginica versicolor versicolor
[76] versicolor versicolor versicolor versicolor versicolor
[81] versicolor versicolor versicolor virginica versicolor
[86] versicolor versicolor versicolor versicolor versicolor
[91] versicolor versicolor versicolor versicolor versicolor
[96] versicolor versicolor versicolor versicolor versicolor
[101] virginica virginica virginica virginica virginica
[106] virginica virginica virginica virginica virginica
[111] virginica virginica virginica virginica virginica
[116] virginica virginica virginica virginica virginica
[121] virginica virginica virginica virginica virginica
[126] virginica virginica virginica virginica virginica
[131] virginica virginica virginica virginica virginica
[136] virginica virginica virginica virginica virginica
[141] virginica virginica virginica virginica virginica
[146] virginica virginica virginica virginica virginica
Levels: setosa versicolor virginica
$correct # 判別の正誤
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[11] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[21] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[31] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[41] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[51] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[61] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[71] FALSE TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[81] TRUE TRUE TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUE
[91] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[101] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[111] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[121] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[131] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[141] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
$correct.table # 判別結果表
prediction
group setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 3
virginica 0 0 50
$correct.ratio # 正判別率
[1] 98
$group
[1] setosa setosa setosa setosa setosa
[6] setosa setosa setosa setosa setosa
[11] setosa setosa setosa setosa setosa
[16] setosa setosa setosa setosa setosa
[21] setosa setosa setosa setosa setosa
[26] setosa setosa setosa setosa setosa
[31] setosa setosa setosa setosa setosa
[36] setosa setosa setosa setosa setosa
[41] setosa setosa setosa setosa setosa
[46] setosa setosa setosa setosa setosa
[51] versicolor versicolor versicolor versicolor versicolor
[56] versicolor versicolor versicolor versicolor versicolor
[61] versicolor versicolor versicolor versicolor versicolor
[66] versicolor versicolor versicolor versicolor versicolor
[71] versicolor versicolor versicolor versicolor versicolor
[76] versicolor versicolor versicolor versicolor versicolor
[81] versicolor versicolor versicolor versicolor versicolor
[86] versicolor versicolor versicolor versicolor versicolor
[91] versicolor versicolor versicolor versicolor versicolor
[96] versicolor versicolor versicolor versicolor versicolor
[101] virginica virginica virginica virginica virginica
[106] virginica virginica virginica virginica virginica
[111] virginica virginica virginica virginica virginica
[116] virginica virginica virginica virginica virginica
[121] virginica virginica virginica virginica virginica
[126] virginica virginica virginica virginica virginica
[131] virginica virginica virginica virginica virginica
[136] virginica virginica virginica virginica virginica
[141] virginica virginica virginica virginica virginica
[146] virginica virginica virginica virginica virginica
Levels: setosa versicolor virginica
$ngroup
[1] 3
二群のときには，二群の重心への距離の差を求め，グラフを描く
> (result <- quad.disc(iris[51:150, 1:4], iris[51:150, 5]))
判別結果
prediction
group versicolor virginica
versicolor 47 3
virginica 0 50
正判別率 = 97.0 %
> plot(result)
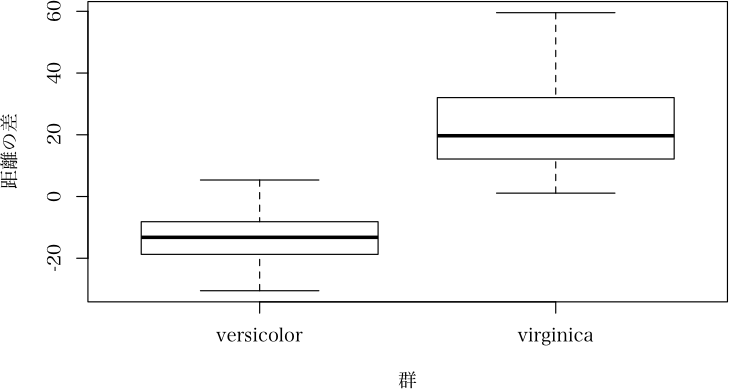> plot(result, which="barplot")
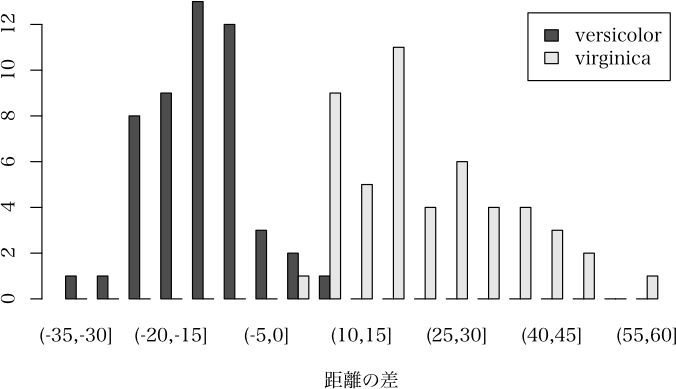> plot(result, which="s", xpos="right")
解説ページ
直前のページへ戻る E-mail to Shigenobu AOKI
