主成分分析 Last modified: Aug 02, 2009
目的
主成分分析を行う。
R には，princomp および prcomp という，二種類の関数が用意されている。
しかし，これらが返す「loadings」は固有ベクトルそのものであって，いわゆる負荷量ではない。
そこで，princomp2，prcomp2 という関数を書いたので，そちらも参照してみるとよい。
使用法
pca(dat)
print.pca(obj, npca=NULL, digits=3)
summary.pca(obj, digits=5)
plot.pca(obj, which=c("loadings", "scores"), pc.no=c(1,2), ax=TRUE, label.cex=0.6, ...)
引数
dat データフレームまたはデータ行列（行がケース，列が変数）
obj pca が返すオブジェクト
npca 表示する主成分数
digits 結果の表示桁数
which 主成分負荷量か主成分得点か
pc.no 描画する主成分番号
ax 座標軸を描き込むかどうか
label.cex 主成分負荷量のプロットのラベルのフォントサイズ
... plot に引き渡す引数
ソース
インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/pca.R", encoding="euc-jp")
# 主成分分析
pca <- function(dat) # データ行列
{
if (is.null(rownames(dat))) rownames(dat) <- paste("#", 1:nrow(dat), sep="")
dat <- subset(dat, complete.cases(dat)) # 欠損値を持つケースを除く
nr <- nrow(dat) # サンプルサイズ
nc <- ncol(dat) # 変数の個数
if (is.null(colnames(dat))) {
colnames(dat) <- paste("X", 1:nc, sep="")
}
vname <- colnames(dat)
heikin <- colMeans(dat) # 各変数の平均値
bunsan <- apply(dat, 2, var) # 各変数の不偏分散
sd <- sqrt(bunsan) # 各変数の標準偏差
r <-cor(dat) # 相関係数行列
result <- eigen(r) # 固有値・固有ベクトルを求める
eval <- result$values # 固有値
evec <- result$vectors # 固有ベクトル
contr <- eval/nc*100 # 寄与率（％）
cum.contr <- cumsum(contr) # 累積寄与率（％）
fl <- t(sqrt(eval)*t(evec)) # 主成分負荷量
fs <- scale(dat)%*%evec*sqrt(nr/(nr-1)) # 主成分得点
names(heikin) <- names(bunsan) <- names(sd) <-
rownames(r) <- colnames(r) <- rownames(fl) <- colnames(dat)
names(eval) <- names(contr) <- names(cum.contr) <-
colnames(fl) <- colnames(fs) <- paste("PC", 1:nc, sep="")
return(structure(list(mean=heikin, variance=bunsan,
standard.deviation=sd, r=r,
factor.loadings=fl, eval=eval,
contribution=contr,
cum.contribution=cum.contr, fs=fs), class="pca"))
}
# print メソッド
print.pca <- function( obj, # pca が返すオブジェクト
npca=NULL, # 表示する主成分数
digits=3) # 結果の表示桁数
{
eval <- obj$eval
nv <- length(eval)
if (is.null(npca)) {
npca <- sum(eval >= 1)
}
eval <- eval[1:npca]
cont <- eval/nv
cumc <- cumsum(cont)
fl <- obj$factor.loadings[, 1:npca, drop=FALSE]
rcum <- rowSums(fl^2)
vname <- rownames(fl)
max.char <- max(nchar(vname), 12)
fmt1 <- sprintf("%%%is", max.char)
fmt2 <- sprintf("%%%is", digits+5)
fmt3 <- sprintf("%%%i.%if", digits+5, digits)
cat("\n主成分分析の結果\n\n")
cat(sprintf(fmt1, ""),
sprintf(fmt2, c(sprintf("PC%i", 1:npca), " Contribution")), "\n", sep="", collapse="")
for (i in 1:nv) {
cat(sprintf(fmt1, vname[i]),
sprintf(fmt3, c(fl[i, 1:npca], rcum[i])),
"\n", sep="", collapse="")
}
cat(sprintf(fmt1, "Eigenvalue"), sprintf(fmt3, eval[1:npca]), "\n", sep="", collapse="")
cat(sprintf(fmt1, "Contribution"), sprintf(fmt3, cont[1:npca]), "\n", sep="", collapse="")
cat(sprintf(fmt1, "Cum.contrib."), sprintf(fmt3, cumc[1:npca]), "\n", sep="", collapse="")
}
# summary メソッド
summary.pca <- function(obj, # pca が返すオブジェクト
digits=5) # 結果の表示桁数
{
print.default(obj, digits=digits)
}
# plot メソッド
plot.pca <- function( obj, # pca が返すオブジェクト
which=c("loadings", "scores"), # 主成分負荷量か主成分得点か
pc.no=c(1,2), # 描画する主成分番号
ax=TRUE, # 座標軸を描き込むかどうか
label.cex=0.6, # 主成分負荷量のプロットのラベルのフォントサイズ
...) # plot に引き渡す引数
{
which <- match.arg(which)
if (which == "loadings") {
d <- obj$factor.loadings
}
else {
d <- obj$fs
}
label <- sprintf("第%i主成分", pc.no)
plot(d[, pc.no[1]], d[, pc.no[2]], xlab=label[1], ylab=label[2], ...)
if (which == "loadings") {
text(d[, pc.no[1]], d[, pc.no[2]], rownames(obj$factor.loadings), pos=1, cex=label.cex)
}
abline(h=0, v=0)
}
使用例
> set.seed(123)
> x <- matrix(rnorm(1000), 100)
> colnames(x) <- paste("X", 1:10, sep="")
> a <- pca(x)
> print(a) # print メソッドによる出力
主成分分析の結果
PC1 PC2 PC3 PC4 PC5 Contribution
X1 0.517 0.477 -0.052 0.047 -0.187 0.535
X2 -0.068 -0.010 -0.443 -0.643 0.328 0.722
X3 -0.306 -0.251 -0.289 0.069 0.467 0.462
X4 0.513 -0.579 0.179 -0.186 0.168 0.694
X5 -0.502 -0.309 0.474 -0.063 -0.432 0.763
X6 -0.337 0.125 0.410 -0.669 0.004 0.744
X7 -0.037 -0.158 -0.525 -0.125 -0.529 0.598
X8 0.557 0.214 0.200 -0.424 -0.107 0.587
X9 -0.181 0.520 0.330 0.150 0.382 0.580
X10 0.371 -0.461 0.327 0.136 0.186 0.510
Eigenvalue 1.477 1.290 1.239 1.143 1.047
Contribution 0.148 0.129 0.124 0.114 0.105
Cum.contrib. 0.148 0.277 0.401 0.515 0.620
> plot(a) # plot メソッドにより，以下のような図を描くことができる
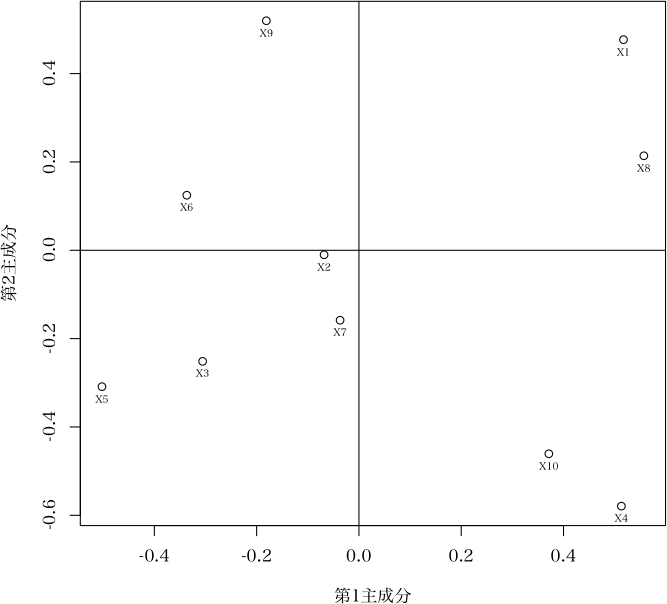> summary(a) # summary メソッドは，すべての結果を表示する
$mean # 平均値
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
0.090406 -0.107547 0.120465 -0.036223 0.105851 -0.042300 -0.149644 0.105874 0.093590 -0.019193
$variance # 分散
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
0.83323 0.93506 0.90227 1.07907 0.97881 0.88121 1.05727 1.02012 1.10630 1.04108
$standard.deviation # 標準偏差
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
0.91282 0.96699 0.94988 1.03878 0.98935 0.93873 1.02824 1.01001 1.05181 1.02033
$r # 相関係数行列
X1 X2 X3 X4 X5 X6 X7 X8 X9
X1 1.000000 -0.049532 -0.1291760 -0.044079 -0.1927111 -0.056484 -0.03436677 0.18157297 -0.022603
X2 -0.049532 1.000000 0.0305790 0.043833 -0.1306222 0.114488 0.07811288 -0.03312350 -0.045328
X3 -0.129176 0.030579 1.0000000 -0.044866 -0.0248484 0.018210 0.00868518 -0.11502946 -0.053282
X4 -0.044079 0.043833 -0.0448657 1.000000 -0.0192599 -0.089913 -0.06378733 0.16789328 -0.165068
X5 -0.192711 -0.130622 -0.0248484 -0.019260 1.0000000 0.206618 -0.00650252 -0.14065351 -0.039583
X6 -0.056484 0.114488 0.0182101 -0.089913 0.2066177 1.000000 -0.06469260 0.09415014 0.074363
X7 -0.034367 0.078113 0.0086852 -0.063787 -0.0065025 -0.064693 1.00000000 0.00026531 -0.128910
X8 0.181573 -0.033123 -0.1150295 0.167893 -0.1406535 0.094150 0.00026531 1.00000000 -0.000812
X9 -0.022603 -0.045328 -0.0532819 -0.165068 -0.0395835 0.074363 -0.12891005 -0.00081201 1.000000
X10 0.011005 -0.091490 -0.0144420 0.245212 -0.0160433 -0.025055 -0.02046957 0.02425240 -0.022721
X10
X1 0.011005
X2 -0.091490
X3 -0.014442
X4 0.245212
X5 -0.016043
X6 -0.025055
X7 -0.020470
X8 0.024252
X9 -0.022721
X10 1.000000
$factor.loadings # 主成分負荷量
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9
X1 0.517278 0.476861 -0.052369 0.046502 -0.1869609 0.285421 -0.077013 0.489319 0.368549
X2 -0.068118 -0.010183 -0.443158 -0.642999 0.3283064 -0.345063 -0.136811 0.220083 0.141827
X3 -0.305558 -0.251422 -0.288849 0.068673 0.4666195 0.664353 0.214749 -0.061908 0.209696
X4 0.513138 -0.579260 0.178953 -0.186259 0.1683695 -0.116629 -0.173785 -0.209851 0.331968
X5 -0.502346 -0.308797 0.473858 -0.063168 -0.4317162 0.033310 -0.114150 0.041986 0.371840
X6 -0.336515 0.124599 0.409766 -0.668959 0.0036195 0.206013 0.166547 0.221193 -0.161331
X7 -0.036841 -0.158350 -0.525102 -0.125233 -0.5292793 -0.137064 0.581665 -0.073112 0.141855
X8 0.557055 0.213936 0.200370 -0.423696 -0.1074629 0.266109 0.181577 -0.454372 -0.060737
X9 -0.181014 0.519696 0.330143 0.149726 0.3820022 -0.351764 0.390861 -0.180442 0.330547
X10 0.371304 -0.460744 0.327348 0.135656 0.1861430 -0.105584 0.471437 0.441483 -0.150436
PC10
X1 -0.050095
X2 0.267016
X3 0.047445
X4 -0.328692
X5 0.288470
X6 -0.332676
X7 -0.139382
X8 0.314292
X9 -0.038484
X10 0.196728
$eval # 固有値
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10
1.47679 1.29035 1.23907 1.14254 1.04747 0.92354 0.88806 0.82569 0.63012 0.53637
$contribution # 主成分距率
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10
14.7679 12.9035 12.3907 11.4254 10.4747 9.2354 8.8806 8.2569 6.3012 5.3637
$cum.contribution # 累積寄与率
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10
14.768 27.671 40.062 51.487 61.962 71.198 80.078 88.335 94.636 100.000
$fs # 主成分得点
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8
#1 -1.612555 -0.273815 -1.6185782 1.08688059 0.2832542 1.092703 0.8801606 -0.89722227
#2 -0.843994 -0.182274 -2.2869553 1.11084435 0.8932829 0.327667 -0.5543246 0.25070182
#3 0.043907 1.585518 0.1595640 0.05497306 0.0034773 0.038015 0.6262311 1.70524691
#4 -0.306952 0.515026 1.4935579 0.32611764 1.3911034 0.333032 0.9030307 1.01841905
#5 -0.148867 -0.744177 -0.2274698 2.14464144 -0.9172497 -1.052776 0.6208851 0.73431644
中略
#99 -0.6323143 -0.332812
#100 -0.9801591 -0.419919
attr(,"class")
[1] "pca"
> b <- pca(iris[1:4])
> plot(b, which="scores", col=c("black", "red", "blue")[as.integer(iris[,5])],
+ pch=c(19, 1, 2)[as.integer(iris[,5])]) # 主成分得点の描画
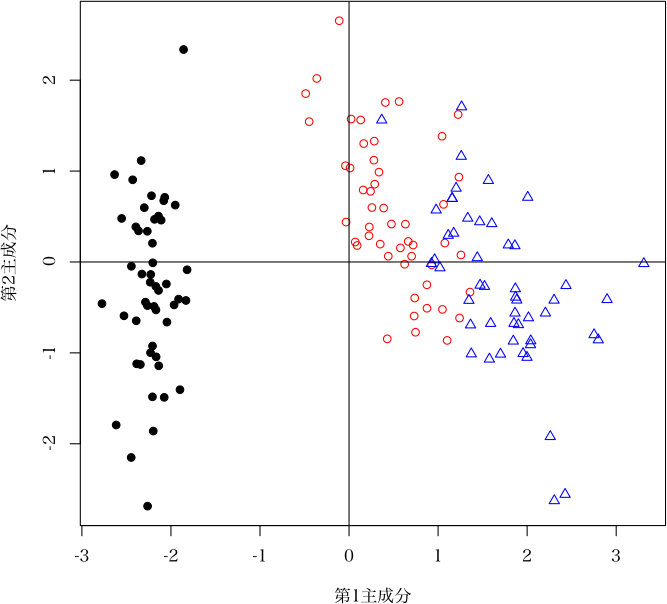（正準判別分析の結果と比較してみよ）
解説ページ
直前のページへ戻る E-mail to Shigenobu AOKI
