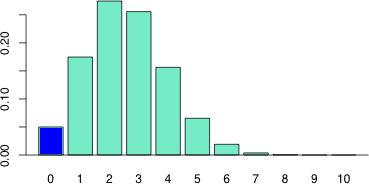
図 1. この関数により得られる推定値での二項分布
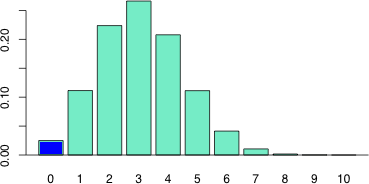
図 2. R の binom.test 関数により得られる推定値での二項分布
目的
母比率の信頼区間を求める。
R には binom.test が用意されており,検定と同時に区間推定も行える。
使用法
prop.conf(r, n, conf=0.95, approximation=FALSE)
引数
r 標本のうち,注目している特性を持つものの数
n 標本の大きさ
conf 信頼率(信頼度)。パーセント表現ではないので注意。
approximation 正規分布による近似を行う場合のみ TRUE を指定する。
ソース
インストールは,以下の 1 行をコピーし,R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/prop_conf.R", encoding="euc-jp")
# 母比率の信頼区間
prop.conf <- function( r, # 標本のうち,注目している特性を持つものの数
n, # サンプルサイズ
conf=0.95, # 信頼率(信頼度)
approximation=FALSE) # 正規分布による近似を行う場合に TRUE を指定する
{
p <- r/n # 標本比率
alpha <- 1-conf # α
if (p == 0) { # 標本比率が 0 の場合
pl <- 0
pu <- 1-alpha^(1/n)
}
else if (p == 1) { # 標本比率が 1 の場合
pl <- alpha^(1/n)
pu <- 1
}
else if (approximation) { # 正規分布による近似を行う場合
z <- qnorm(alpha/2, lower.tail=FALSE) # 両側確率がαになる Z 値
x <- n/(n+z^2)*(p+z^2/(2*n)+c(1, -1)*z*sqrt(p*(1-p)/n+z^2/(4*n^2)))
pu <- x[1]
pl <- x[2]
}
else { # F 分布を使って正確な信頼区間を求める場合
nu1 <- 2*(n-r+1)
nu2 <- 2*r
Fv <- qf(alpha/2, nu1, nu2, lower.tail=FALSE)
pl <- nu2/(nu1*Fv+nu2)
nu1 <- 2*(r+1)
nu2 <- 2*(n-r)
Fv <- qf(alpha/2, nu1, nu2, lower.tail=FALSE)
pu <- nu1*Fv/(nu1*Fv+nu2)
}
setNames(c(pl, pu), c("lower.p", "upper.p"))
}
使用例
prop.conf(0, 10)
prop.conf(10, 10)
prop.conf(175, 500, approximation=TRUE)
prop.conf(175, 500)
出力結果例
> prop.conf(0, 10) # 標本比率が 0 の場合
lower.p upper.p 信頼限界の下限値と上限値
0.0000000 0.2588656
標本比率が 0 になる場合,ここで作成したプログラムは,標本中に注目している特性を持つものが全くいない確率が 0.05 になるときの母比率の推定値を返す(図 1)。
> dbinom(0:10, 10, p=0.2588656)
[1] 4.999997e-02 1.746414e-01 2.744966e-01 2.556719e-01 1.562782e-01
[6] 6.550238e-02 1.906572e-02 3.805332e-03 4.984266e-04 3.868709e-05
[11] 1.351274e-06
> binom.test(0, 10) # R の binom.test による結果
Exact binomial test
data: 0 and 10
number of successes = 0, number of trials = 10, p-value = 0.001953
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.0000000 0.3084971 # 信頼区間
sample estimates:
probability of success
0
R では,上に示したように計算した場合は,alternative="two.sided" が仮定されるので,標本中に注目している特性を持つものが全くいない確率が 0.025 になるときの母比率の推定値を返す(図 2)。> dbinom(0:10, 10, p=0.3084971) [1] 2.500000e-02 1.115314e-01 2.239065e-01 2.663744e-01 2.079638e-01 [6] 1.113335e-01 4.139061e-02 1.055166e-02 1.765262e-03 1.750063e-04
 図 1. この関数により得られる推定値での二項分布 |
 図 2. R の binom.test 関数により得られる推定値での二項分布 |
> binom.test(0, 10, alternative="less")
Exact binomial test
data: 0 and 10
number of successes = 0, number of trials = 10,
p-value = 0.0009766
alternative hypothesis: true probability of success is less than 0.5
95 percent confidence interval:
0.0000000 0.2588656
sample estimates:
probability of success
0