目的

指定した平均値行列 mu と標準偏差行列 sigma，相関係数ベクトル r を持つ母集団から，
比率ベクトル prob で抽出される n 組の混合 2 変数正規乱数を発生させる

使用法

mix2(n, mu, sigma, r, prob=rep(1/length(mu),length(mu)))

引数

n      データ組数
mu     平均値行列（グループ×2変数）
sigma  標準偏差行列（グループ×2変数）
r      相関係数ベクトル（グループ）
prob   抽出割合（グループ）

ソース

アルゴリズムは 1 変数の場合を参照

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/mix2.R", encoding="euc-jp")

# 指定した平均値ベクトル mu と標準偏差ベクトル sigma を持つ母集団から，比率ベクトル prob で抽出される n 個の混合正規乱数を発生させる
mix2 <- function(    n,                                      # データ組数
                        mu,                                     # 平均値行列（グループ×2変数）
                        sigma,                                  # 標準偏差行列（グループ×2変数）
                        r,                                      # 相関係数ベクトル（グループ）
                        prob=rep(1/length(mu),length(mu)))      # 抽出割合（グループ）
{
        library(MASS)
        k <- nrow(mu)
        if (k == nrow(sigma) && k == length(r) && k == length(prob) &&
            ncol(mu) == 2 && ncol(sigma) == 2) {
                suffix <- sample(k, n, replace=TRUE, prob=prob)
                x <- mapply(function(mean1, mean2, sd1, sd2, r) {
                        cat(mean1, mean2, sd1, sd2, r, "\n")
                        mvrnorm(n, mu=c(mean1, mean2),
                                Sigma=matrix(c(sd1^2, r*sd1*sd2, r*sd1*sd2, sd2^2), 2),
                                empirical=TRUE)},
                        mu[,1], mu[,2], sigma[,1], sigma[,2], r)
                dim(x) <- c(n, 2, k)
                return(list(d=t(mapply(function(i, k) x[i,,k], 1:n, suffix)), which=suffix))
        }
}


使用例

以下のような平均値，標準偏差，相関係数を持つ 3 個の母集団から 6:3:1 の割合で標本抽出する

平均値行列　mu <- matrix(c(50, 60, 45, 50, 65, 48), byrow=TRUE, ncol=2)

　　　　　　変数1　変数2
第1母集団     50     60
第2母集団     45     50
第3母集団     65     48

標準偏差行列　sigma <- matrix(c(8, 3, 7, 4, 2, 2), byrow=TRUE, ncol=2)

　　　　　　変数1　変数2
第1母集団      8      3
第2母集団      7      4
第3母集団      2      2

相関係数　r <- c(0.8, 0.6, 0.3)

第1母集団  0.8
第2母集団  0.6
第3母集団  0.3

> set.seed(123)
> n <- 10000
> mu <- matrix(c(50, 60, 45, 50, 65, 48), byrow=TRUE, ncol=2)
> sigma <- matrix(c(8, 3, 7, 4, 2, 2), byrow=TRUE, ncol=2)
> r <- c(0.8, 0.6, 0.3)

> d <- mix2(n, mu, sigma, r, prob=c(6,3,1)) # データは要素名 d に入る

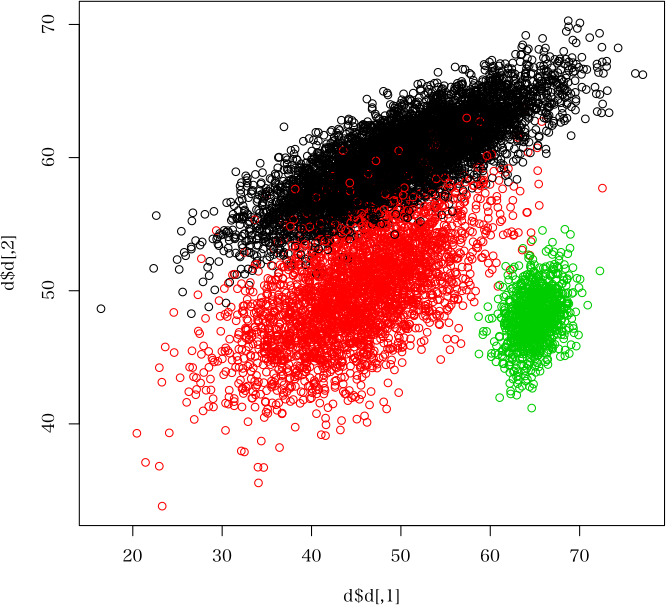
> plot(d$d, col=d$which) # データを描画

> d2 <- split(data.frame(d$d), d$which) # グループごとのデータに分解

> sapply(d2, nrow) # データ数の確認
   1    2    3 
6047 3008  945 

> sapply(d2, colMeans) # 平均値の確認
          1        2        3
X1 49.96261 45.13133 64.94212
X2 59.99781 50.02271 48.04493

> sapply(d2, function(z) apply(z, 2, sd)) # 標準偏差の確認
          1        2        3
X1 8.021501 6.961244 1.980484
X2 2.991986 4.017926 2.027641

> sapply(d2, function(d) cor(d[,1], d[,2])) # 相関係数の確認
        1         2         3 
0.7996692 0.6028584 0.2976533