 |
ある厚みにペンキを塗るようにペンキ屋さんにお願いをします。ペンキ屋さんはいわれた厚みmになるように意識してペンキを塗ります。もちろん塗り残しや,とんでもなく厚く塗ることはありません。数日後,ペンキが乾いてからペンキの厚さを何箇所かで測定すると,測定値はmより大きかったり小さかったりです。ペンキは厚さmに塗れたといえるのでしょうか。
ペンキ屋さんは何箇所かの値を平均してその値がmに近いことから指示通りの塗装であるといいますが私は疑問でした。
そこで,私は高校生の時習った正規分布を思い出して,参考書を片手に区間推定を行ってみたのです。
その計算をある人に見せたら,「塗装の塗膜の厚さは正規分布しない」というのです。「意図的にある厚さを狙って塗るわけだし,第一,正規分布だとまったく厚さがゼロだとかいったことも考慮するけど,ペンキは現に全面に塗れているんだからそんなことはあり得ない」と言うのです。
統計をここ数日ちょっとかじったばかりで混乱しているのですが,正規分布をペンキの厚さの推定に用いるのが間違っているのでしょうか。ペンキの厚さが正規分布でないにしても,正規分布に良く似た分布をする気がしますし・・・
何か大きな勘違いをしてるかもしれないのですが,ペンキの厚みを何点かを測定して区間推定するのは正しいでしょうか。
ペンキを重ね塗した場合(下塗と上塗)に,下塗が乾いた時点で厚みを測定して,上塗が乾いた時点で厚みを測定しました。上塗の厚さだけを区間推定することはできないですよね。上塗の厚さはどうやって測ればいいでしょう。現時点では上塗までの平均値から下塗の厚みの平均値を減ずる方法しかなく,区間推定のしようがありません。
ペンキが乾く2週間の間に,この問題を解決したいのです。
正規分布を規定するパラメータは平均値と標準偏差の 2 つです。
意図的であるということは「厚さを狙って塗る」わけで,極端に薄くするとか厚いところと薄いところを作るという意味での意図的ではないわけです。前者の場合は要するにペンキの厚さのばらつきは「偶然の誤差を伴う」ということになり,これがまさしく正規分布を生み出します。正規分布を発見したガウスは「誤差分布」という言葉を使っていたと思います。
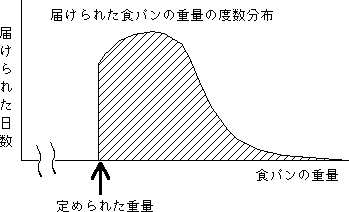
この類例としてよく挙げられるものに,「不誠実なパン屋の話」があります。
出入りのパン屋が届ける食パンの重量がいつも不足しているのに気がついたとき,実際に毎日食パンの重量を測り,平均値を出します。
また,毎日食パンの重量を測ります。
また,毎日食パンの重量を測ります。
 |
この客は統計学者だったので,「このパン屋は不誠実である。誠実なパン屋は定められた重量を平均値として,ばらつきがなるべく小さくなるようにすべきである。そのようにしたとき,平均以下の重量のパンが届くのは50%くらいはあるはずだ。もっとも,その場合でも許容できる重量不足の程度は問題とする。」と,結論づけました (^_^;)
さて,ちょっと話がずれました。
誠実なペンキ屋さんが塗ったペンキの厚さが,平均値 0.5mm,標準偏差 0.02mm だとします。これはたぶん正規分布すると思います(確かめるためには50ポイントあるいはもっと多くのポイントでの測定値の分布図を描くといいでしょう)。
あなたが相談した人の言うように「厚さが 0 のところはない」はずです。なぜかと言えば,たくさんのポイントで測定したとき,厚さが 0 であるポイントが存在する確率は, 3.056×10-138です(^_^;)... ほとんど0でしょう。これはちょっと極端すぎる例ですので,厚さが 0.44mm 以下のポイントの存在する確率を計算してみると,それは 0.00135 です。これを求めるためには,標準化得点 Z を使います。
ある測定値−平均値 標準化得点 = ----------------------- 標準偏差
例に挙げた場合では Z = (0.44-0.5)/0.02 = -3 ですね。標準正規分布(平均値が 0,分散が 1 )において Z が -3 以下になる確率は 0.00135 です(Z が 3 以上になる,すなわちペンキの厚さが 0.56 以上になる確率も同じです)。Z の絶対値が大きくなると,そのようなことが生じる確率は非常に急速に 0 に近づくのです。この意味で,あなたが相談した人の言った「正規分布は,まったく厚さがゼロだとかいったことも考慮するからだめだ」ということは,理論上は正しいのですが,実際上は的外れです。(その人の言うことをもっと極端に言えば,正規分布ではペンキの厚さがマイナスの場合だって考えないといけません。なんといっても,正規分布は−∞から+∞までに分布するのですから)
結論としては,いくつかのデータを採取して,それが正規分布と大幅に異なっていない(分布が左右対称のきれいな山形である---程度でいいと思います)ならば,正規分布を仮定して,標本からの平均値と標準偏差に基づいて信頼区間を求めてよいということです。
これは実はできると思います。
下塗りが終わったときの計測値を x1, x2, ..., xn,上塗りが終わったときの計測値(上塗りと下塗りの合計)を z1, z2, ..., zn,とします。
あなたは,「xi と同じポイントで yi を測っていないからだめではないか」と考えたわけでしょうが,実は同じポイントで測られていなくてもよいのです。
上塗りだけの真の計測値があったとします。これを y1, y2, ..., yn とします。
あなたは,「上塗りだけの計測値がないからだめだろう」と考えましたが,そんなことはありません。
これ以降の話には,「演算子 E, V」 も参照してください。
「真の上塗りのみの厚さ」の平均値 Y は y1, y2, ..., yn(これは測定されていないので未知です)から求めます。下塗りのみの厚さの平均値 X は x1, x2, ..., xn(既知)から求めます。下塗りと上塗りの合計(上塗り後の測定値)の平均値 Z は z1, z2, ..., zn(既知)から求めます。
では,y1 = z1-x1, y2 = z2-x2, ..., yn = zn-xn ですから,
Y = (y1+y2+...+yn)/n = {(z1-x1)+(z2-x2)+...+(zn-xn)}/n
= (z1+z2+...zn)/n - (x1+x2+...+xn)/2
= Z - X
つまり,ある測定値 Ai と Bi があったとき,Ci=Ai±Bi を計算したとき,
平均値[C] = 平均値[A] ± 平均値[B] 復号同順
また,ついでに,分散は
分散[C] = 分散[A] + 分散[B] 必ず和(+)であるがなりたちます。
厳密に言えば上の分散の関係式は「測定値 A と B が無相関である」ことが必要です。
(より一般的に言えば,
分散[C] = 分散[A] + 分散[B] ± 共分散[A,B]
無相関のときは,共分散[A,B]=0なので...)
これにより,真の上塗りのみの厚さ y1, y2, ..., yn の分散の推定値は,下塗りと上塗りの合計の厚さ z1, z2, ..., zn の分散から,下塗りのみの厚さ x1, x2, ..., xn の分散を引いたものになります。
よって,下塗り完了時点と上塗り完了時点の平均値と分散がわかっていれば,上塗りだけの厚さの平均値と分散がわかりました。これで,上塗りの厚さの信頼区間を求めることができます。
なお,下塗りの厚さと真の上塗りの厚さが無相関かどうかということですが,これはなかなか難しいと思います。
2回の測定場所が対応していないと言うことは無相関であろうという推測の補強になるのですが,ペンキ塗りの場合には他の要素が入ってきそうに思います。素人考えながら,下塗りが薄い部分(へこんでいる部分)は上塗りは厚くなりそうですし,下塗りが厚い部分(周りより高い部分)の上塗りは薄くなりそうです。