まず,例を見てもらいましょう。

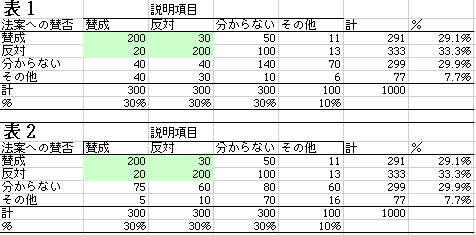
> ある法案に対し、「賛成」29.1%、「反対」33.3%、「わからない」29.9%、「その他」7.7%の、回答が寄せられた場合
ということで,全例数を1000にして,周辺度数を固定します。
つぎに,
> 他のどの質問項目が、法案の賛否と最も強い関わりを持つかを調べる
ということで,この項目がどういう選択肢を持つか,またその分布がどうかは分かりませんが,一応,「賛成」、「反対」、「わからない」がそれぞれ30%、「その他」10%と仮定しましょう。
表1も,表2も,法案に賛成か反対か,また,その態度を説明する項目(同じような選択肢としたがそれはどうでもいい)も賛成か反対かという明確に答えたものに色つけをした。
該当する人数は全体の45%にしかならないことに注意。その人達にしか注目しないからというなら,それでもいいのかもしれないが,私は,残りの人たちのことも気になる。
色を付けた部分(2×2分割表)だけに注目してスピアマンの順位相関係数を計算すると 0.7783561(理論的に,ピアソンの積率相関係数,ケンドールの順位相関係数も全く同じ値です)。かなり強い相関になっている。
「賛成」,「反対」,「その他」の3×3分割表として,クラメール係数を計算してみると,表1では0.466062496,表2では0.394107999ということになる(ちなみに,2×2分割表のクラメール係数はピアソンの積率相関係数と理論的に同じ値になる)。
表1では,要するに法案への賛否を「分からない」と答える人は,説明項目も「分からない」と答える傾向にあるということ。例えばそれは,要するに何にも分かってない人たちないしは,調査に非協力的・無責任な人たちということかもしれない。
表2では,法案への賛否に「分からない」と答える人たちは,説明項目においては,いろいろな意見を持っている人たちということ。
この二つの表を,双対尺度で分析してみると以下のようになる。
表1の分析結果
第01軸 第02軸 第03軸
相関比の二乗 0.35378 0.18934 0.00375
相関係数 0.59479 0.43513 0.06126
寄与率 % 64.7 34.6 0.7
累積寄与率 % 64.7 99.3 100.0
カイ二乗値 434.644 208.964 3.743
自由度 5 3 1
P 値 0.00000 0.00000 0.05304
★ 最適重みベクトル --- 相関比による重み付けをしないもの
行 第01軸 第02軸 第03軸
R01 1.41427 0.26887 -0.60330
R02 -1.03117 0.90073 -0.35831
R03 -0.38287 -1.51475 0.08493
R04 0.49837 0.71040 3.14243
列 第01軸 第02軸 第03軸
C01 1.49549 0.30347 0.06897
C02 -0.92004 1.14090 0.43036
C03 -0.45406 -0.77712 -1.23420
C04 -0.36415 -2.00176 2.20462
表2の分析結果
第01軸 第02軸 第03軸
相関比の二乗 0.34937 0.13732 0.03567
相関係数 0.59108 0.37057 0.18887
寄与率 % 66.9 26.3 6.8
累積寄与率 % 66.9 93.2 100.0
カイ二乗値 427.883 147.048 36.160
自由度 5 3 1
P 値 0.00000 0.00000 0.00000
★ 最適重みベクトル --- 相関比による重み付けをしないもの
行 第01軸 第02軸 第03軸
R01 1.39125 0.53001 -0.46896
R02 -1.10167 0.87646 -0.14537
R03 0.06651 -0.82573 1.39647
R04 -0.55731 -2.16852 -1.97178
列 第01軸 第02軸 第03軸
C01 1.45734 0.45658 -0.03220
C02 -1.01611 1.07910 0.36933
C03 -0.41898 -0.93287 -1.13470
C04 -0.06673 -1.80845 2.39271
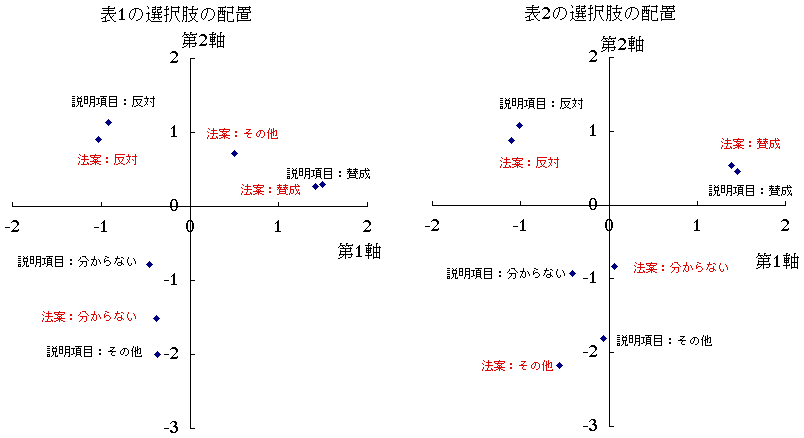
法案について「分からない」はいずれの場合においても法案「賛成」と「反対」の中間どころにあるということがわかった。第2軸において,法案「その他」がずいぶんと違った位置にあることが分かる。
結局,例としてあげた二つの表に限っても,3×3分割表としてみれば,これだけの違いがあるということです。