No.23097 Re: 生存時間解析におけるハザード関数とCIF 【波音】 2021/07/19(Mon) 13:28
ご返信ありがとうございます。
下川先生からの回答は得られていないのですが,下記書籍に明確な回答となるような記述がありましたのでご共有します(今後,同じような悩みを持った方に向けて)。
---
参考図書
神田・藤井・古川(訳)「エモリー大学クラインバウム教授の生存時間解析」サイエンティスト社(2015)
---
まず,
>言葉上はハザード関数とCIFは何か似ていることを言っているような,,,
という点ですが,以下のように考えれば分かりやすいかと思われます。
【前提】
1) 生存関数S(t)とハザード関数h(t)は明確な関係があり,S(t)からh(t),あるいは逆の変換が可能。 →参考図書P15
2) ハザード関数によって出力される値は「確率ではなく」,得られる値は「使用する時間の単位によって異なる数値」になる可能性がある。つまり1.0を超えることがある。 →参考図書P13
この2つの前提を元に,私が理解できた事実は以下のとおりです:
■
ハザード関数とCIFは「違う」ものである,ということ。
数学的(計算的)に,ハザード関数は前提1に示す通り「1.0を超える」が,CIFは確率なので1.0を超えない。
■
そして,このCIFは
リスクが1つしかない(競合リスクがない)場合は「1 - KM」となる
ということです。 →参考図書P447に記載
※競合リスクがある場合は,CIFは競合別ハザード関数から導かれ,競合イベントの存在下でイベントの「周辺確率」推定値を与えるので,上記のように1-KMで計算された値は大きくか,小さく見積もられることがあるようです。
■
したがって,最初の私の質問にある
>色々な情報の中に「1 - 生存確率(Kaplan-Meier)はいけない」と書かれているようです。これは競合リスクがある場合に限定されるのでしょうか
という点については,競合リスクがないと仮定できる場合はOK,そうでない場合はNG,ということになります。
※ちなみに,RでCIFを用いる場合は下記URL資料P13に記載があるので,これを参照。
http://nfunao.web.fc2.com/files/R-intro/R-stat-intro_13.pdf
具体例としては↓のように。
fit <- cuminc(dat$経過時間, dat$目的変数, dat$カテゴリカル型変数)----- 以下補足
a <- timepoints(fit, times=dat$経過時間)
cif <- t(a$est[1:2, ])
write.csv(cif, "CIF.csv")
>商品を「購買したかどうか」ということに生存時間分析を用いてアプローチしたいです。
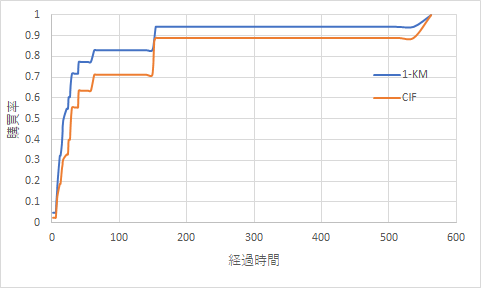
という点についてですが,実データに近いサンプルデータを用意して出力した結果を添付しました。
私の抱えていた問題は「どの時点で購買率が頭打ちになるか」ということだったので,結論としては(盛り上がりの曲線形状がほぼ同じなので),1-KMだろうがCIFだろうが,どちらも得られる知見は同じでした。
ただ,たしかに利用分野などで「発症率」や「再発率」のような問題を扱う場合は,形状が同じでも縦軸の差が大きな意味を持つので,CIFを用いた方がよい(1-KMは不適切という書籍に書かれている通り)と思われます。