「統計学関連なんでもあり」の過去ログ--- 048

No.23019　ピアソンの相関係数とコサイン類似度　　【明石】　2021/02/01(Mon) 11:16

青木先生　様；

お忙しいところを失礼いたします，明石と申します。

毎々，ご丁寧なご教示をいただき，誠にありがとうございます。
改めて御礼を申し上げます。
ありがとうございます。

初歩的な質問で大変に恐縮していますが，ご教示をいただきたいと思います。
何卒どうぞよろしくお願いいたします。

---------------------------------------------------------------

記事No.23016
連続変数とカテゴリカル変数／ダミー変数が混在した場合の相関係数
で，
点双列相関係数を教えていただきました。

これを契機に，今まで考えたことがなかった，
類似度（相関），非類似度（距離）について調べながら，Rで追試しています。

大変に初歩的な質問で申し訳ございません。

連続量からなるデータフレームでは，ピアソンの相関係数で計算します。

類似度を測るものとして，コサイン類似度があります。

ピアソンの相関係数ではなく，コサイン類似度で計算すると，何か問題があるのでしょうか？

分かりませんので，ご教示をいただけましたら助かります。

お手数をおかけします。
//

No.23020　Re: ピアソンの相関係数とコサイン類似度　　【aoki】　2021/02/01(Mon) 15:15

コサイン類似度は
R で書くと
COS = function(a, b) sum(a * b) / sqrt(sum(a ^ 2)) / sqrt(sum(b ^ 2))
ですね。
相関係数は，COS を使って書くと，
COR = function(a, b) COS(a-mean(a), b-mean(b))
になります。

以下で検算
> a = c(1, 3, 2, 4, 5, 2, 3, 4, 5, 6)
> b = c(2, 1, 2, 3, 5, 4, 3, 3, 3, 4)
> COS(a, b) # コサイン類似度
[1] 0.937391
> COR(a, b) # 相関係数
[1] 0.5477226
> cor(a, b) # 相関係数（いつも使っている関数）
[1] 0.5477226
コサイン類似度は相関係数より大きめに出ていますね。
大ざっぱに説明すると，コサイン類似度は原点からの距離，相関係数は平均値からの距離に基づくわけで，
> sum(a*b)
[1] 114
> sqrt(sum(a ^ 2))
[1] 12.04159
> sqrt(sum(b^2))
[1] 10.0995

> sum((a-mean(a))*(b-mean(b)))
[1] 9
> sqrt(sum((a-mean(a)) ^ 2))
[1] 4.743416
> sqrt(sum((b-mean(b)) ^ 2))
[1] 3.464102
のように，前者の方が大きいのです。

それで，
> 114/12.04159/10.0995
[1] 0.9373918
> 9/4.743416/3.464102
[1] 0.5477226
の違いになるのです。
この例だけだと，ふーんと思うだけかも知れませんが，
COS = function(a, b) sum(a * b) / sqrt(sum(a ^ 2)) / sqrt(sum(b ^ 2))
COR = function(a, b) COS(a-mean(a), b-mean(b))
sim = function(trial = 500, n = 10, mean = 50, sd = 10) {
    res_cos = numeric(trial)
    res_cor = numeric(trial)
    for (i in 1:trial) {
        a = rnorm(n, mean, sd)
        b = rnorm(n, mean, sd)
        res_cos[i] = COS(a, b)
        res_cor[i] = cor(a, b)
    }
    plot(res_cos, res_cor)
    legend("topleft", legend=sprintf("mean = %d", mean))
}
layout(matrix(1:4, 2))
par(mgp=c(1.8, 0.8, 0), mar=c(3, 3, 1, 1))
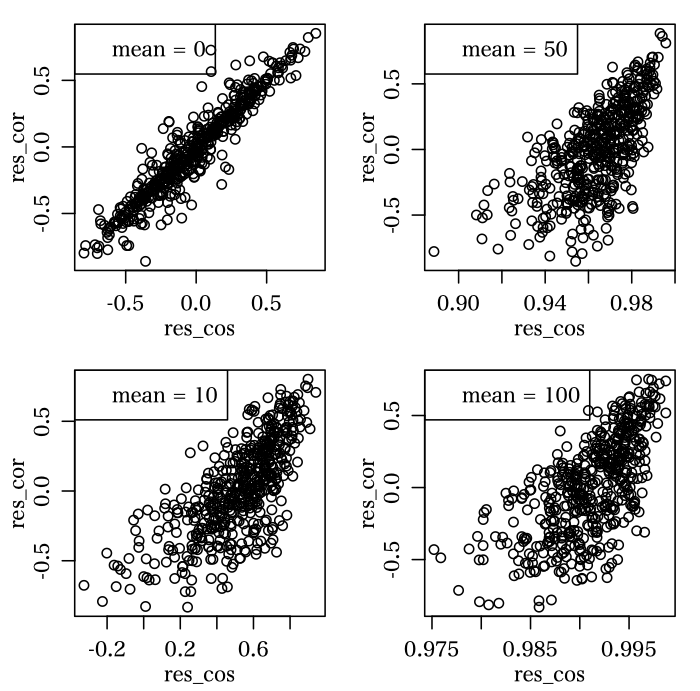
sim(mean=0, sd=10)
sim(mean=10, sd=10)
sim(mean=50, sd=10)
sim(mean=100, sd=10)
layout(1)
のようなプログラムを書いてシミュレーションしてみるとちょっと驚くでしょう。

平均値が大きくなるにつれ（つまり，データのまとまりが原点から遠くにあるほど）コサイン類似度は大きくなります（当然ですが，相関係数はそんなことはありません）。

また，一般的には，コサイン類似度は対象間の類似度を表すために使われることが多いと思います。

No.23021　Very Special Thanks!!（Re: ピアソンの相関係数とコサイン類似度）　　【明石】　2021/02/01(Mon) 17:03

青木先生　様；

お忙しいところを失礼いたします，明石と申します。

大変にご丁寧にご教示してくださり，とてもよく分かりました。
ありがとうございました。

青木先生にお聞きする前に，Google先生にお聞きしましたら，
幾つか，この話題に関するサイトが見つかりましたが，
納得感がなく，理解できませんでした。

勇気を振り絞って，青木先生にお聞きしてよかったです。
納得でき，よく理解できました。
//