No.22982 相関係数につきまして 【アメリ—】 2020/11/17(Tue) 11:59
たびたび申し訳ございません。
相関係数について,勉強しており,量×量なのですが,片方が正規分布,もう片方が正規分布しておらず,F分布のような分布です。
この場合,Pearson を使うより,Spearman の方がよろしいでしょうか?
試しに両方やったら,両方,有意差があり,同じ結果で相関ありとなりました。
お手数をお掛け致しますが,どうぞよろしくお願い致します。
No.22984 Re: 相関係数につきまして 【アメリ—】 2020/11/18(Wed) 10:40
補足ですが,片方が 1 2 3 4 5 6の正規分布データ,もう片方が1〜29までの非正規分布のデータなので,Spearman の順位相関係数で検定しようと思います。
もし,間違っていたら,ご教授いただければ幸いです。
お手数をお掛け致しますが,どうぞよろしくお願い致します。
No.22986 Re: 相関係数につきまして 【aoki】 2020/11/18(Wed) 22:54
相関係数についての今回の質問は,二つの変数が正規分布するかどうかではなく,ピアソンの積率相関係数は直線相関
を見るのに対して,スピアマンの順位相関係数は曲線相関を見るという対比ではないかと思われますが。まあ,片方の変数が大きな値を取りがち(あなたのいう
F分布類似のような分布)の場合は,直線相関等よりは曲線相関っぽくなるでしょうが)。
両者の違いは,正規分布するかしないかの問題はではないで
しょう。つまり,ピアソンの積率相関係数は,両者が正規分布に従うかどうかは要件にしていないでしょう。もとの変数が y = a*x + b
なのか,あるいは,たとえば y = f(x) ,たとえば y=c * x^d とか の曲線相関かどうかということ。
正規分布するかしないかは,極端な数値が現れやすいかどうかということにも関係しますが(極端な値があると,ピアソンの積率相関係数は大きくなりやすい。極端な場合は,わずか1個の極端な値のために相関係数が1に極めて近い値になる事もある)。
以
下の例は y2 = y^3 / 1e4
としたものですが,曲線相関と直線相関の違いについての例示です。大小関係を測定するスピアマンの順位相関係数は両者で全く同じになりますが,直線相関を
求めるピアソンの積率相関係数はちいさくなります。つまり,曲線相関の場合は,ピアソンの積率相関係数はスピアマンの順位相関係数より小さな値になりま
す。
まあ,両者を計算して,どちらも有意な相関係数という結果になったのなら,どちらでもよいでしょうが,それぞれの相関係数が何を測定
しているのかは理解して置いた方がよいでしょう。つまり,あなたは,二変数の相関関係において,曲線相関を想定したのか,直線相関を想定したのかという根
本的な前提意識があったのかどうかということです。これは,重要なことですよ。二変数の間の因果関係に関連することですから。モデルの違いですよね。単
に,二つの変数が正規分布するかどうかなんてことではないです。相関関係は二つの変数がどんな分布に従うかどうかなんてあまり重要なことではないです。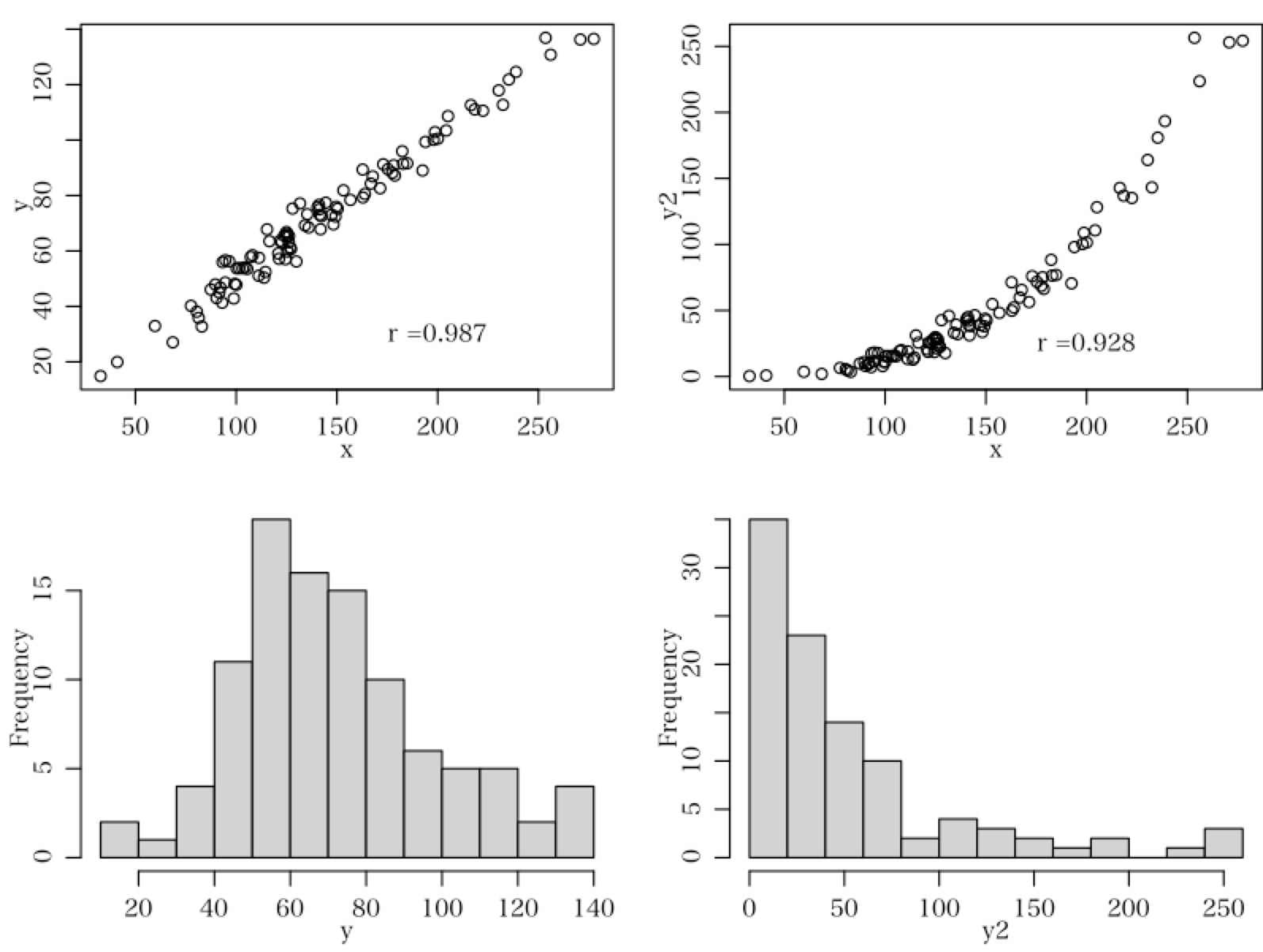
No.22988 Re: 相関係数につきまして 【アメリ—】 2020/11/19(Thu) 12:41
青木先生
お返事,どうもありがとうございました。
とっても勉強になりました。
実際の所,先生のお示しくださった右側の図のようなF分布が1つと,ほぼ富士山型の分布のデータが1つで,その相関をみたいと思いました。
ただ,1〜6まで,6が最強と考え,スピアマンの順位相関係数を算出したところ,rs=0.12となり,ほぼ相関なしとなりました。
ただ,1〜6までの数値データと,2カテゴリー(良い・悪い)にしたχ2検定では,有意さが見られ,検定はどれを表示すべきか,混乱しており,ご教授いただけませんでしょうか?
厚かましいお願いで大変申し訳ございません。お手数をお掛け致しますが,どうぞよろしくお願い致します。
ここまで書いて気が付いたのですが,F分布と富士山では,相関なしで当たり前ですよね。。。バカみたいな質問で,大変申し訳ございません。
● 「統計学関連なんでもあり」の過去ログ--- 048 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る
