No.22813 Re: 教育心理 重回帰 ロジスティック 【青木繁伸】 2019/08/23(Fri) 14:21
その本の著者も,学会(査読者?)も間違えています。間違ったことを書いているクソページもたくさんありますね。
前に説明したことに基づいて,反論しなかったのですか?
説 明変数は正規分布しなくても差し支えありません。ダミー変数を説明変数に使う場合を考えて見ればわかるでしょう。ダミー変数は 0/1 の二値データで,正規分布などしません。カテゴリーデータは重回帰分析に使えない(使うなら数量化 I 類を使いなさい)などという,とんでもない時代錯誤の考えを持っている人もまだいるのだろうか?また,実験計画によるデータの場合,説明変数は特定の値を 取ります(薬剤投与量と効果の場合,薬剤投与量は例えば 10mg, 20mg, ..., 100mg などとされるでしょう。だれも薬剤投与量を正規乱数から選ぼうなどとは思わないでしょう)。
目的変数は,正規分布しなくても構いません。正規分布しないといけないのは残差の分布です(さらに,それさえも必須条件ではない)。
誤差が正規分布しないと,予測値の信頼区間を求めることができないからです。誤差(測定誤差も含む)は普通は正規分布に従うものです。なので,統計分析できるのです。
日本語のページは信頼できないということなら,英語のページを検索してはいかがでしょうか。
https://www.statisticssolutions.com/assumptions-of-multiple-linear-regression/
Multiple regression assumes that the residuals are normally distributed.
http://www.restore.ac.uk/srme/www/fac/soc/wie/research-new/srme/modules/mod3/3/index.html
Normally distributed residuals: The residuals should be normally distributed.
https://www.m3.com/open/clinical/news/article/604122/
回 帰式の形は,被説明変数のタイプによって変えることができます。被説明変数が連続変量の場合は重回帰分析,2値変数(時間依存性がないイベントの発生また は非発生,死亡または生存,治癒または非治癒など)の場合はロジスティック回帰分析,打ち切りのある2値変数の場合はCox回帰分析を用います。
重回帰分析では,残差(回帰分析による予測値と実測値の差分)の分布が正規分布である必要があります。
https://bellcurve.jp/statistics/course/9700.html
回帰モデルを考えるにあたって,誤差 μi にはいくつかの仮定している条件があります。
1. μi の期待値は0である
2. μiの分散は常にσ2 である
3. 異なる誤差 μi,μj は互いに独立である
これらの3条件から,μi は互いに独立に正規分布 N(0, σ2) に従うと仮定されます。
==================================
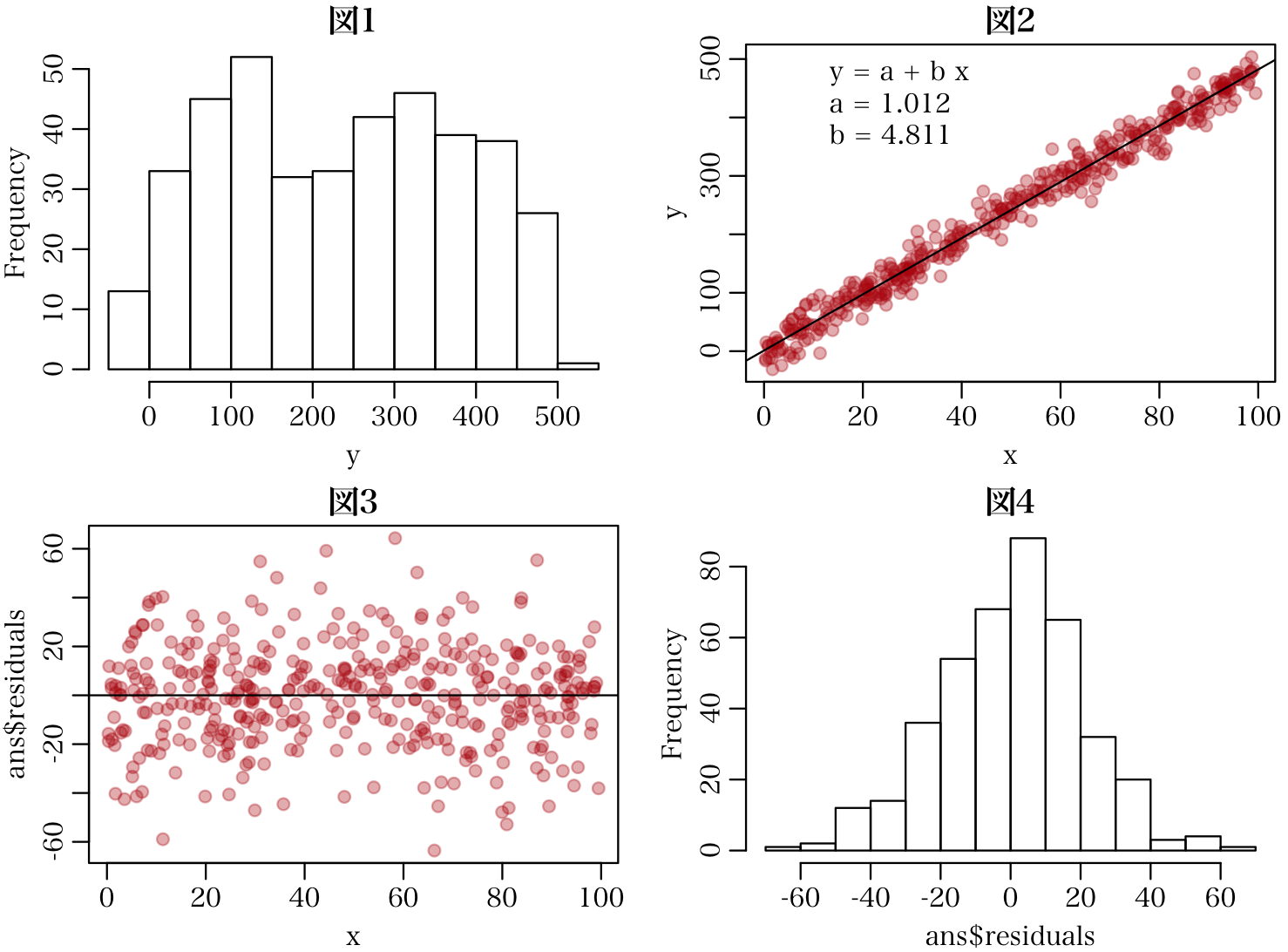
具体例でも示してみましょう。正規分布すべきは「残差」です。
理論モデル y = 2.5 + 4.8 * x
重回帰モデルは y = a + b * x + ε
εが正規分布
データを用意する
n = 1000y は正規分布しない!!
x = runif(n, min=0, max=100) # 独立変数
EPSILON = rnorm(n, mean=0, sd=10) # ε:正規分布
y = 2.5 + 4.8 *x + EPSILON # 誤差を含む従属変数
hist(y, main="図1")予測は十分
plot(y ~ x, pch=19, col="#aa000055", alpha=0.3, main="図2")誤差(予測誤差)は正規分布する
ans = lm(y ~ x)
summary(ans)
abline(ans)
text(10, 400, sprintf("y = a + b x\na = %.3f\nb = %.3f", ans$coef[1], ans$coef[2]), pos=4)
plot(ans$residuals ~ x, pch=19, col="#aa000055", main="図3")図は,クリックすることで拡大表示
hist(ans$residuals, main="図4")