No.22767 Re: ダミー変数を従属変数にした場合の切片 【青木繁伸】 2019/06/30(Sun) 07:19
従属変数が 0/1 の二値データであることと,切片が負の値を取ることは何の矛盾もありません。
というか,独立変数のとる値により切片は負の値になることも,[0, 1] の値になることも,1より大きな値になることもあります。
たとえば,
d <- data.frame(y = c(1, 0, 1, 1, 0, 0, 0, 1, 0, 0),の場合は,切片は負の値になります。
x1 = c(58, 37, 38, 50, 36, 59, 49, 66, 47, 58),
x2 = c(54, 53, 50, 46, 46, 65, 37, 69, 37, 44))
> lm(y~x1+x2, data=d)ここで,x1 から 250 を引いた変数 x1.250 を作り,それを用いて予測式を計算すると
(Intercept) x1 x2
-0.646540 0.005094 0.015825
> d$x1.250 <- d$x1 - 250ここで,x1 から 435 を引いた変数 x1.435 を作り,それを用いて予測式を計算すると
> lm(y~x1.250+x2, data=d)
(Intercept) x1.250 x2
0.627073 0.005094 0.015825
> d$x1.435 <- d$x1 - 435それぞれの偏回帰係数は全く同じになっていることに注意。
> lm(y~x1.435+x2, data=d)
(Intercept) x1.435 x2
1.569546 0.005094 0.015825
つまり,独立変数の平行移動をした場合,その影響を打ち消すために定数項が調整されるということ(ちなみに独立変数を定数倍したときは偏回帰係数が定数分の1になる)。
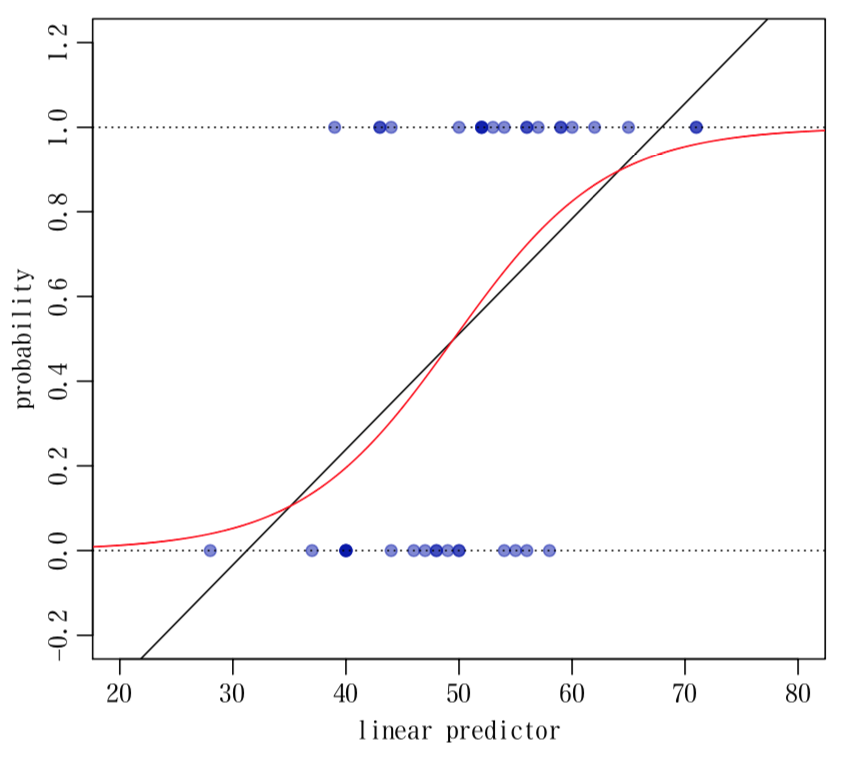
で,今回の問題の本質は,なぜ従属変数が 0/1 の二値データなのに予測値が0より小さくなったり,1より大きくなったりしてしまうのかということ。
それは直線回帰をするからやむを得ないということです。
図を見れば明らかです。
二値データはロジスティック回帰分析を行うのが定石です。
図の赤で示したのがロジスティック曲線です。
> glm(y~x1+x2, data=d, family=binomial(link="logit"))
Call: glm(formula = y ~ x1 + x2, family = binomial(link = "logit"),
data = d)
Coefficients:
(Intercept) x1 x2
-5.08999 0.02083 0.07214
Degrees of Freedom: 9 Total (i.e. Null); 7 Residual
Null Deviance: 13.46
Residual Deviance: 11.93 AIC: 17.93