「統計学関連なんでもあり」の過去ログ--- 048

No.22030　非正規分布の検定について　　【下山】　2016/06/18(Sat) 18:43

度々お世話になります。

ある要素Aの有無に対してスコアB(%)，スコアC(%)というN=150程度の表が有ります。
A B C
有 10% 17%
無 15% 18%
有 20% 28%
・・・

A- B，A-Cについてそれぞれ要素Aの有無とスコアの間に差が有るか，有るとすればどちらが大きいかを検定したいと考えています。B，Cの分布は正規性検定ではどちらも非正規という結果でしたので，U検定をしようかと思いました。U検定ではBもCもP<0.01でした。分散分析を行ったところA-Bは有無の2群間で分散は等しくなく，A-Cは等分散という結果になりました。

A-Cは中央値で評価しようかと思いましたが，A-Bについては有群と無群どちらがスコアが高いかをどう評価しようか，と壁に当たりました。
どのような方法がありますでしょうか？中央値を用いても良いのでしょうか？

もし正規性の検定以降の手順についても，間違っているところがありましたらご指摘いただけましたら大変ありがたく存じます。どうぞよろしくお願いいたします。

No.22031　Re: 非正規分布の検定について　　【青木繁伸】　2016/06/18(Sat) 20:32

そもそも，

> A B C
> 有 10% 17%
> 無 15% 18%
> 有 20% 28%
> ・・・・

というデータの見方がわかりません。

それと，検定に必要なのは，% ではなく，実数です。
本当のデータ（実数）が明らかになって困るとは思えないので，それぞれが何を表すかは言う必要はないのだから，ちゃんと説明する方がよいと思いますけど？
じゃないと，返答のしようがない。

No.22032　Re: 非正規分布の検定について　　【下山】　2016/06/19(Sun) 08:38

青木先生，失礼いたしました。
BとCはそれぞれ異なる計算式から算出した予測死亡率で，どちらもいくつかの調査項目から計算しています。ですので％単位になっています。

取り急ぎお返事させていただきました。

No.22033　Re: 非正規分布の検定について　　【青木繁伸】　2016/06/19(Sun) 17:49

検定できないでしょう

No.22034　Re: 非正規分布の検定について　　【下山】　2016/06/19(Sun) 20:39

青木先生ご回答ありがとうございます。
このデータに関しては検定できない，ということで分析から外す方向で考えます。

後学のために以下のような場合にどう評価していくかも教えていただけましたらありがたく存じます。

N=150
A=某塾に通っているかどうか
B=期末試験の点数（通塾の有無で分けた場合等分散ではない）
C=統一模試の点数（通塾の有無で分けた場合等分散である）

として，点数がどちらも正規分布していない場合，通塾の有無で期末試験の点数に差があるか，あるとすればどちらが点数が高い傾向があるのか，および通塾の有無で統一模試の点数に差があるか，あるとすればどちらが点数が高い傾向があるのかを評価したい。この場合であればデータは実数となるかと思いますが，ご教授いただけましたらありがたく存じます。
大変恐縮でございますが，どうぞよろしくお願いいたします。

No.22035　Re: 非正規分布の検定について　　【青木繁伸】　2016/06/19(Sun) 21:04

この例と，前のと，どのような関係があるのですか？
本当は関係がないのに，別の問題だとして回答したことを（つまり，新たに提示されたデータについてはこれこれの検定が適切でしょうということを），あなたが勝手に（状況は全く違う）この問題にも適用するかもしれないという懸念があるのに，回答できないでしょう？

抽象的なことばかり言っていないで，データの性質も含めて記述しないと，なんの回答もできません（私のせいにされるのは心外で，そんなことこわくて，できません）。

No.22036　Re: 非正規分布の検定について　　【下山】　2016/06/20(Mon) 14:06

青木先生

検定を根本的に理解しておらず多々考え違いをしていることを痛感いたしました。ご気分を害してしまいましたことお詫びいたします。

理解が乏しい中で自分なりに解釈すると，正規分布が仮定できる場合にしろ分割表にしろ非正規分布の場合にしろ，実際のデータを吟味しないといけなくて，初心者向けの統計本に記載されているような，パラメトリックなら対応の有無を考慮してt検定やANOVAで，分割表ならχ二乗で，ノンパラメトリックなら・・・で，というように馬鹿の一つ覚えで1対1に決めてできるものではないということかと考えました。

必要十分なデータの性質についての情報を記載できる自信はありませんが(データの性質といわれても自分には分布や分散，外れ値くらいしか思いつかない程度の理解で)，添付の画像のようなデータです。Logitはそれぞれ異なる論文に記載されていた回帰式より計算しております。

はじめに先生がご回答されたように，こういうデータは検定できないのでしょうか(あるいは検定を行う意味・意義がない，検定すべきではない)。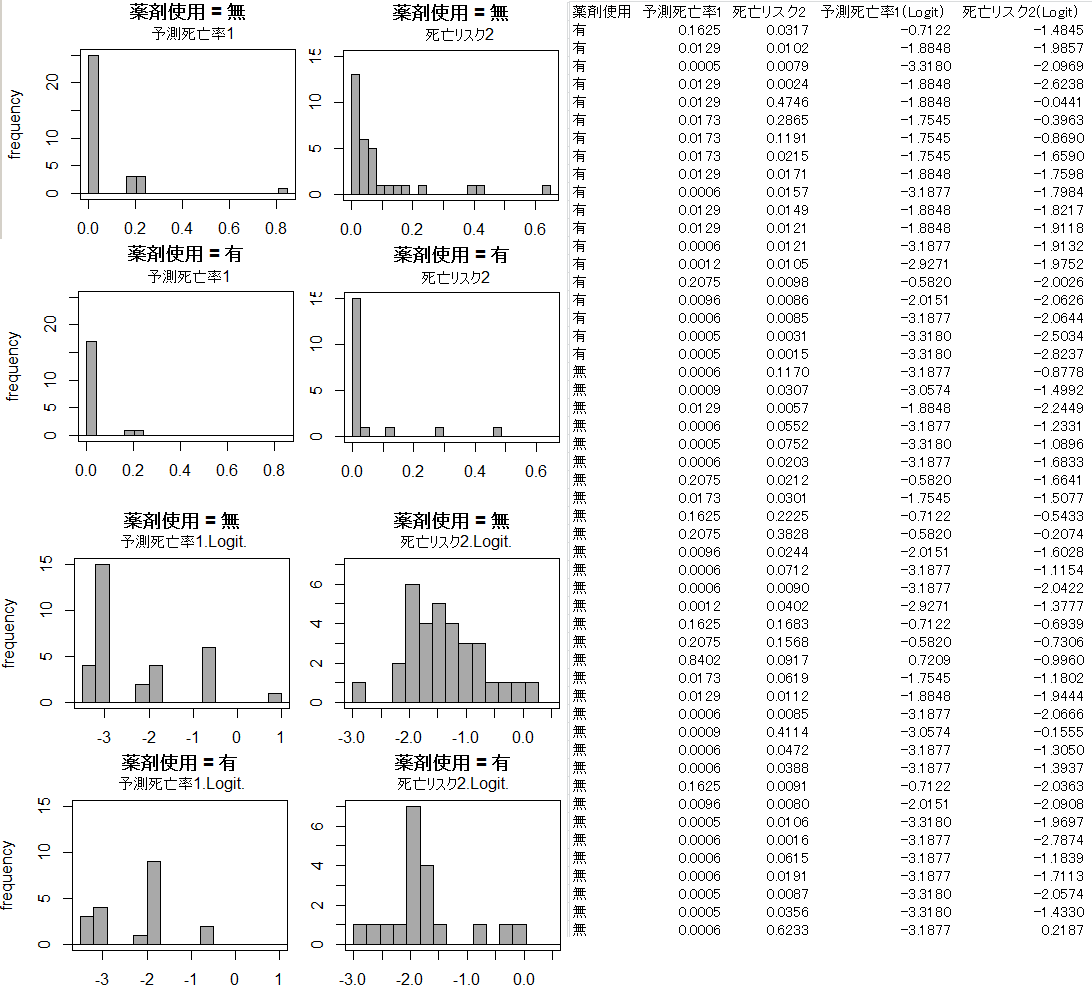

No.22037　Re: 非正規分布の検定について　　【鈴木康弘】　2016/06/22(Wed) 07:15

　せっかく具体的なデータを出していただいたのに，一般論ですが，
　正規分布し分散も等しい2変数を利用して，2群に差があるかを検定するなら，多変量分散分析を使うはずです。

　でもこの条件に合わなければこれは使えない。
　だから2変数を一度に使うことはあきらめざるをえない（と思う）。

　正規分布もしてないし分散も異なる2群を単変量で検定するのだったら，Brunner-Munzel検定というのがあるようです。

No.22038　Re: 非正規分布の検定について　　【下山】　2016/06/22(Wed) 20:12

鈴木先生

御助言ありがとうございます。Brunner-Munzel検定は初めて聞きました。
調べてみたいと思います。