「統計学関連なんでもあり」の過去ログ--- 045

No.16119　変数を標準化して交互作用項を作るとき　　【波音】　2011/12/30(Fri) 00:39

変数x1と変数x2をそれぞれ標準化してからx3=x1*x2という変数を作ると，x1とx3，x2とx3の相関が0になるのはなぜでしょうか？

x1 <- 1:10
x2 <- 1:10
x3 <- x1 * x2

x1.2 <- scale(x1)
x2.2 <- scale(x2)
x3.2 <- x1.2 * x2.2

plot(x1, x3)
points(x1.2, x3.2, col="red")

のようにすれば，イメージ的にも分かりますし，標準化してかければマイナス同士がプラスになるので相関係数は0に近くなるのもなんとなく納得できます。

しかし数式的に（数学的に）説明するとどういうことなのかしっくりきません。。。

どなたかこの現象を説明してくださいませんか？

No.16122　Re: 変数を標準化して交互作用項を作るとき　　【青木繁伸】　2011/12/30(Fri) 08:24

> plot(x1, x3)
> points(x1.2, x3.2, col="red")

で描かれた図は，実態を正確に表現したものではありません。赤い○が x1.2, x3.2 ですが，x1.2 の範囲は
> range(x1.2)
[1] -1.486301 1.486301
なのに，x1.2 が正の部分しか描かれていません。負の部分も含めて描くと，添付図左のようになり，その部分を拡大すると右の図になります。x1.2 と x2.2 が等しいため，x1.2 * x2.2 = x1.2^2 となります。右の散布図の相関係数が（正確に）0になることは自明ですね。

No.16128　Re: 変数を標準化して交互作用項を作るとき　　【波音】　2011/12/31(Sat) 15:02

ご返答ありがとうございます。

なるほど，自乗のグラフ（放物線）になるから相関係数は0になるのは当たり前ですね（確かに考えてみればそれはそうか・・・）。

---
http://harp.lib.hiroshima-u.ac.jp//bitstream/harp/4876/1/hjt4307.pdf

の一説に「元の変数を標準化して交互作用項を作成すると，元の変数（X1, X2）と交互作用項（X1*X2）の相関が小さくなるので，主効果と交互作用効果の多重共線性を回避できる」という記述があります。

単相関を見て多重共線性が生じるかどうかが分かるのかという問題とかもありますが，それはともかくとして，仮にそうだとしても元の変数を標準化してもそこから作られた交互作用項との相関が十分に小さくなるとは限らないような気がしているのです。

例えば以下のような例：
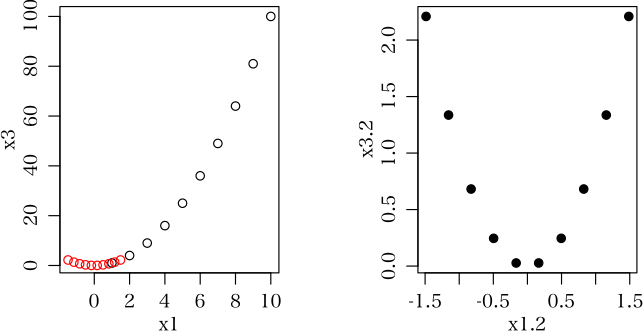
> x1 <- 1:10
> x2 <- c(2, 6, 8, 12, 22, 19, 30, 33, 20, 10)
> cor(cbind(x1, x2, x3))
          x1        x2        x3
x1 1.0000000 0.6154986 0.7737062
x2 0.6154986 1.0000000 0.9458568
x3 0.7737062 0.9458568 1.0000000
> 
> x1.2 <- scale(x1)
> x2.2 <- scale(x2)
> x3.2 <- x1.2 * x2.2
> cor(cbind(x1.2, x2.2, x3.2))
           [,1]       [,2]       [,3]
[1,]  1.0000000  0.6154986 -0.5892743
[2,]  0.6154986  1.0000000 -0.1103786
[3,] -0.5892743 -0.1103786  1.0000000
これだとx1とx2を標準化して，新たにx1.2*x2.2の交互作用項を作ったところでx1.2とx3.2の相関関係はさほど小さくならなっていません（x2.2とx3.2の相関係数は十分に小さくなっていますが）。もちろん，先の例のようにx1もx2もどちらも単調増加（あるいは単調減少）するようなケースでは相関係数が小さくなりますが，そうでないケースもあると思うのです。

そもそも主効果と交互作用項の多重共線性を回避するための操作としてどうなのか，という懸念も無きにしも非ずのような気もしますが・・・

No.16133　Re: 変数を標準化して交互作用項を作るとき　　【青木繁伸】　2011/12/31(Sat) 21:15

失礼。直前のコメントを削除し訂正版をアップします
色々な例はありうるでしょうが，一般的には提示されたことは正しいと思われます。
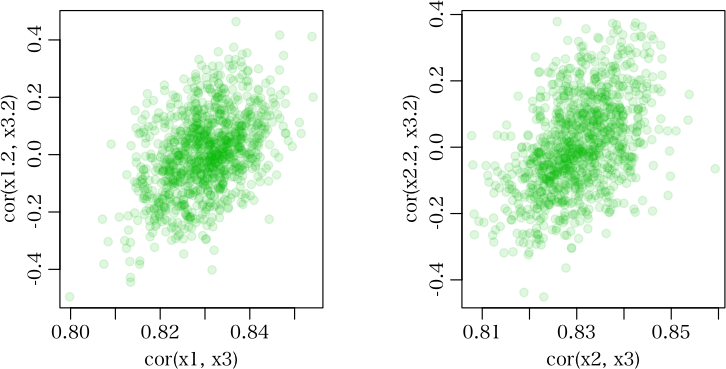
スケール（中心化）前後の相関係数の比較です。
> sim <- function()
+ {
+ 	x <- gendat2(100, 0.4)
+ 	x1 <- x[,1]*10+50
+ 	x2 <- x[,2]*20+100
+ 	x3 <- x1*x2
+ 	x1.2 <- scale(x1)
+ 	x2.2 <- scale(x2)
+ 	x3.2 <- x1.2 * x2.2
+ 	return(c(cor(x1, x3), cor(x1.2, x3.2), cor(x2, x3), cor(x2.2, x3.2)))
+ }
> result <- replicate(1000, sim())
> layout(matrix(1:2, 1))
> par(mgp=c(1.8, 0.6, 0))
> plot(result[1,], result[2,], xlab="cor(x1, x3)", ylab="cor(x1.2, x3.2)", col="#00aa0020", pch=19)
> plot(result[3,], result[4,], xlab="cor(x2, x3)", ylab="cor(x2.2, x3.2)", col="#00aa0020", pch=19)
> layout(1)
ただし，多重共線性が生じるかどうかは単相関係数によって判定されるものではないと言うことは肝に銘じておくべし。
No. 16050 からのスレッドで，独立変数間の相関係数が 0.8 であっても，多重共線性が生じない例を挙げている。

No.16148　Re: 変数を標準化して交互作用項を作るとき　　【波音】　2012/01/03(Tue) 20:44

回答ありがとうございます。

うーん，なるほど。元の変数を標準化して交互作用項をつくると，結果として元の変数と交互作用項の相関係数が低くなることもある，と。そしてそれがマルチコ回避にもなるということもある，という事実はあるわけですね。

こういう操作はあくまでも1つの手段として「ありうる」というだけで，万能な方法ではないようですね(^_^;)