No.15375　分析方法について　　【春名】　2011/09/24(Sat) 23:31

初めまして。私は大学院で劣等感についての研究を行っています。

「A：他者と比較して自己の劣性を認知」 したときに，「B：劣等感が生じる」といわれていますが，劣性を認知したからといって必ずしも強い劣等感を抱くわけではなく，「C：自己意識特性」が関係 しているのではないかと考えています。（劣性を認知しやすい人が強い劣等感を抱くとは限らない）

A→C→Bという因果関係になるのですが，Cはクラスター分析でいくつかのクラスターに分けられます。そのCのクラスター（タイプ）によって，劣性を認知したときに生じる劣等感の強さに差がみられると予想しています。
クラスターごとにA→C→Bの効果をみて，クラスター間比較でどのCのタイプの人が劣性を認知したときにより強い劣等感を抱きやすいかを調べたいです。
また，A→Bの効果よりもA→C→Bの効果の方が大きいということも検証したいのですが，このような場合どの分析手法を用いればよいでしょうか。

ご回答よろしくお願い致します。わかりづらいところがあればご指摘ください。
No.15378　Re: 分析方法について　　【波音】　2011/09/25(Sun) 12:04

文章を読んだ印象に過ぎませんが，最も単純には各クラスターごとに「B = A（AはBを説明するという回帰分析モデル）」を解析することになるのではないでしょうか。もう少しいえば，クラスタというカテゴリカル変数をモデルに取り入れた共分散分析モデルの解析でしょう。

　B = A + C（BはAとCによって説明される，という意味です）

AとBがそれぞれどういう変数（連続型なのかカテゴリカル型なのか）分からないので何とも言えませんが，，，

あるいは流行にのるならSEM（構造方程式モデリング＝共分散構造分析）ではないでしょうか。

>　A→Bの効果よりもA→C→Bの効果の方が大きい

とうことは，換言すれば全体混みで分析するよりもクラスターというカテゴリカル変数をモデルに投入したときの方がモデルの適合度（説明変数が応答変数をより良く説明しているという事実）が高いということでしょう。
No.15384　Re: 分析方法について　　【春名】　2011/09/25(Sun) 20:22

ご回答ありがとうございます。
Aは劣性の認知のしやすさを，Bは劣等感の強さを5件法で回答してもらうので，連続型となります。
統計に関してはかなり不慣れなので，まずはシンプルな方法で考えてみたいのですが，『クラスターごとに「B = A（AはBを説明するという回帰分析モデル）」を解析する』ということは，クラスターごとにパス解析を行うということになるのでしょうか。
ク ラスター内でA→Bの効果と，A→C→Bの効果の比較を行い，Cがあることによる効果の差をみること，そしてクラスター間でA→C→Bの効果を比較して， どのクラスターが劣性を認知したときにより強い劣等感に結びついているかをみるということで，やり方としては間違いないでしょうか。
もし違っていたり，不明瞭な点があればご指摘ください。

また，共分散構造分析の方はこの研究に当てはめるとどのようなことになるのでしょうか。うまく理解しきれておらず申し訳ありません。

ご回答よろしくお願い致します。
No.15386　Re: 分析方法について　　【波音】　2011/09/25(Sun) 22:35

最初の投稿で

>　Cはクラスター分析でいくつかのクラスターに分けられます。

とあったので，Cというのはカテゴリカル変数だと思ったのです。

だ から，もし各クラスタによってAがBを説明する量が大きければ，それはすなわちCというカテゴリカル型変数が重要（あるクラスタはBの影響が他のクラスタ に比べてAに対し大きく効いている）といえるのでは？と思った次第です。もしクラスタが意味のないものであれば，どのクラスタについてもA→Bという影響 度（要は回帰係数）が同じだろうということです。

つまりこの方法は

>　クラスターごとにパス解析を行うということになるのでしょうか。

ということに該当するのだと思います（パス解析というのはいまだに私はよく分からないのですが，この場合は回帰分析になるでしょう）。

>　クラスター間でA→C→Bの効果を比較して，どのクラスターが劣性を認知したときにより強い劣等感に結びついている

前述したように，私はCという変数はクラスタを表すカテゴリカル変数かと思っていたので，，，(^_^;)　少し難しい内容で私にはよく分かっていないようです。

>　共分散構造分析の方はこの研究に当てはめるとどのようなことになるのでしょうか。

私は質問を読んで添付した図のようなパス図が描けるのかなと思いました。

A→C→BというのはSEMでやるのでなければ，1つずつ別のモデルとして解析するしかありません。例えばAが連続型，Cがカテゴリカル型，Bが連続型だとしたら，

　C = A　（目的変数がC，説明変数がA　＝　名義ロジスティック回帰）
　B = C　（目的変数がB，説明変数がC　＝　分散分析）

という2つのモデルを解析することになります（余計混同させるような説明をしてしまったかもしれないという懸念はありますが・・・）。

そしてすみません，明日以降に確実に質問にレスポンスできる保証がないので回答に日が空いてしまうかもしれません。

No.15387　Re: 分析方法について　　【春名】　2011/09/26(Mon) 00:11

重ね重ねご丁寧にありがとうございます。
私自身分析のことをよくわかっていないために，混乱させてしまい申し訳ありません。

Cについては自己意識尺度というものを使って回答を得るのですが，サンプルをクラスター分析にかけて「公的自己意識が高く，私的自己意識が低い群」「公的自己意識が低く，私的自己意識が高い群」といったように分けられる予定です。（おそらく2〜4群）

『だ から，もし各クラスタによってAがBを説明する量が大きければ，それはすなわちCというカテゴリカル型変数が重要（あるクラスタはBの影響が他のクラスタ に比べてAに対し大きく効いている）といえるのでは？と思った次第です。もしクラスタが意味のないものであれば，どのクラスタについてもA→Bという影響 度（要は回帰係数）が同じだろうということです。』
『この場合は回帰分析になるでしょう』

この記述に関しては納得して理解できました。
この方法であれば，どのクラスタ間の差をみることができますよね。
ありがとうございます。なかなか理解できず申し訳ありません。

ただ，単純なA→Bの効果と，クラスタで分けた時のA→Bの効果は比較できないことになるのでしょうか。（そもそも不可能？）
単 に劣性を認知しやすいと強い劣等感を抱きやすいというわけではなく，Cによって差がみられるかもしれない・・・というのをみていきたいので単純なA→Bの 効果もみないといけないのではないかという感じがしてしまい，まだどこか引っかかっている状態です。この部分がSEMにかかわるのでしょうか。
そもそも最初の方に書かれている回帰分析だけで事足りてるのでしょうか。

何度も申し訳ありませんが，ご返答よろしくお願いします。
No.15412　Re: 分析方法について　　【波音】　2011/10/01(Sat) 02:49

日が経っているので自己解決したかもしれませんが。。。

>　この記述に関しては納得して理解できました。

ということと，改めて質問を考えてみるとやはり共分散分析をするということになるのではないでしょうか。文脈からもクラスタ分析を行う目的が応答変数をより良く説明するためのカテゴリカル型の説明変数を作成する，という目的があるように思えます。

つまりこういうこと↓


> cls <- c(1,1,1,1,1, 2,2,2,2,2, 3,3,3,3,3)           # クラスタ変数
> A <- c(12,24,30,10,22, 45,55,66,59,39, 2,3,2,9,5)   # 説明変数
> B <- c(34,44,33,16,22, 11,9,3,8,21, 40,45,41,66,57) # 応答変数
> result <- lm(B ~ A + cls + A:cls)   # 共分散分析
> summary(result)                     # 係数表

Call:
lm(formula = B ~ A + cls + A:cls)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.3051 -2.5403 -0.3103  1.9390 11.4407 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  17.5085     8.4890   2.062   0.0692 .
A             0.6271     0.4043   1.551   0.1553  
cls2         22.9181    18.8851   1.214   0.2558  
cls3         16.5777    10.2368   1.619   0.1398  
A:cls2       -1.1958     0.5121  -2.335   0.0444 *
A:cls3        3.1143     1.2222   2.548   0.0313 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 6.804 on 9 degrees of freedom
Multiple R-squared: 0.9175,     Adjusted R-squared: 0.8716 
F-statistic: 20.01 on 5 and 9 DF,  p-value: 0.0001243 

> summary(aov(result))     # 分散分析表
            Df Sum Sq Mean Sq F value    Pr(>F)    
A            1 3226.0  3226.0 69.6785 1.574e-05 ***
cls          2  657.4   328.7  7.0992  0.014110 *  
A:cls        2  748.0   374.0  8.0776  0.009801 ** 
Residuals    9  416.7    46.3                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

> xv <- seq(0, 70, 1)     # 以下プロットのための記述
> yv.cls1 <- (17.50+0.00) + (0.62+0.00)*xv
> yv.cls2 <- (17.50+22.91) + (0.62+(-1.19))*xv
> yv.cls3 <- (17.50+16.57) + (0.62+3.11)*xv
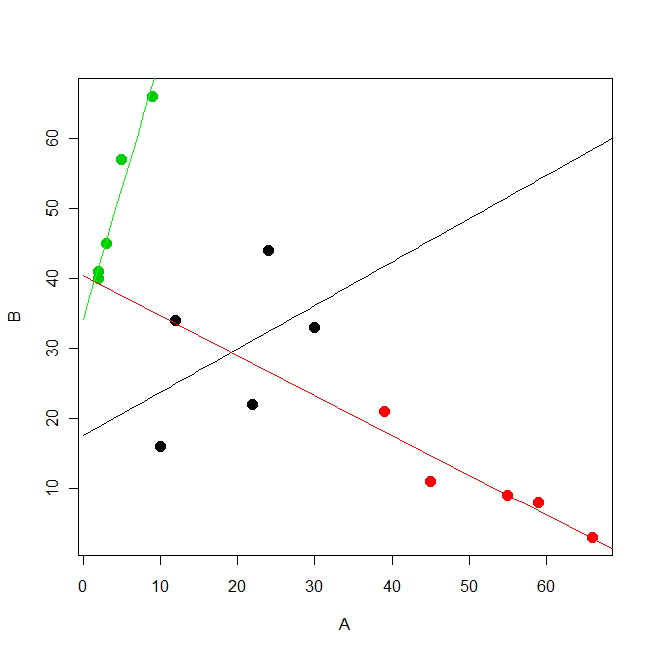
> points(xv, yv.cls1, type="l", col="black")
> points(xv, yv.cls2, type="l", col="red")
> points(xv, yv.cls3, type="l", col="green")

詳しくはRのコードや共分散分析について調べて頂きたいのですが，共分散分析の意味するところは大きく2つあります。

・各群の平均値が有意に異なるか（分散分析）
・各群においてXの増分に対してYの増加，あるいは減少の度合い（傾き）は有意に異なるか（回帰分析）

今 回の例データでは3つのクラスタ間で応答変数Bの平均値が異なることが確認できます（そしてそれは統計的に有意な差が認められる＝分散分析表でclsの項 は有意である）。また，各クラスタによって説明変数Aの増加に伴って，応答変数Bの増減（変化量）も変わります（分散分析表でAの項が有意である）。

結論としてまとめてみると：

・グリーンのクラスタは最もBの平均値が高く，Aが増加するとBも急激に増加する（他のクラスタの回帰係数：傾きが大きい）。

・ブラックのクラスタはグリーンよりも小さく，レッドより大きい。BはAの増加に伴って比較的なだらかに増加していく。

・レッドのクラスタは最もBの平均値が低く，Aが増加するとBは減少する（回帰係数の符号がマイナスである）。

みたいな知見が得られますが，例えば「公的自己意識が高く，私的自己意識の高い群は自己の劣勢認知度が高くなると劣等感が弱くなる」といったようなことが分かるのだと思います。

No.15474　Re: 分析方法について　　【春名】　2011/10/10(Mon) 22:07

ご回答ありがとうございます。

読ませていただいて気付いたことがあります。
私はA劣性の認知の得点が高い人だけを抽出して，
B劣等感の強さのクラスター間の差を見ようとしていました。
しかし，クラスターによってAにも差がみられる可能性がありますよね。

B劣等感はA劣性の認知によって生じる感情なので

＞各クラスタによって説明変数Aの増加に伴って，応答変数Bの増減（変化量）も変わります

という部分はとても重要な前提だと思われます。
それにもかかわらず見落としていました。

本当にありがとうございました。論文提出まであと3か月ほどですが頑張りたいと思います。

● 「統計学関連なんでもあり」の過去ログ--- 044 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る