「統計学関連なんでもあり」の過去ログ--- 044

No.14735　指数分布の確率密度関数　　【統計の子猫】　2011/06/07(Tue) 15:32

指数分布の確率密度関数は，確率変数をxとしたとき，f(x)=m*exp(-m*x) と表記できます。
ここで，m=2，x=0 の場合の計算をすると，f(0)=2.0 となります。
m=2の場合の確率密度を計算すると，ちゃんと1になることも確認しています。
ただ，計算は間違っていないのに，確率が 1 を超える場合があることに，今一つしっくりきません。
この f(0)=2 をどのように理解すれば良いでしょうか？
ご教授お願いいたします。

No.14736　Re: 指数分布の確率密度関数　　【青木繁伸】　2011/06/07(Tue) 16:02

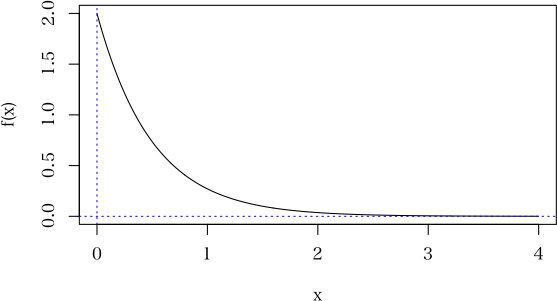
それは，確率ではなく，確率密度です。確率密度の上限値はありません（1 以上の値も取ります）。
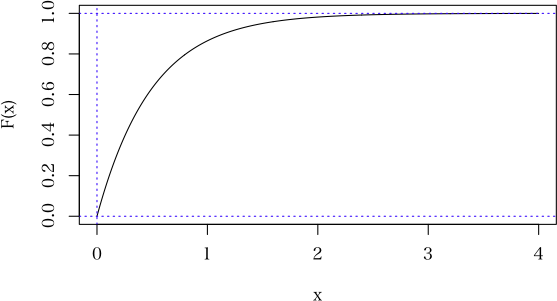
確率密度を積分したものが確率です。
R では，f(x) は dexp 関数で計算，確率は pexp 関数で計算。
0 ～ ∞ 区間での積分は，pexp(0, rate=2, lower.tail=FALSE) で，1 になります。
> x <- seq(0, 4, length=500)
> y <- dexp(x, rate=2)
> plot(x, y, type="l", ylab="f(x)") # 確率密度曲線
> abline(h=0, v=0, col="blue", lty=3)
> (prob <- pexp(0, rate=2, lower.tail=FALSE)) # 0 以上の確率
[1] 1

No.14738　Re: 指数分布の確率密度関数　　【青木繁伸】　2011/06/07(Tue) 16:11

以下は，分布関数 F(x)。つまり，0 から x までの値を取る確率。
> plot(x, pexp(x, rate=2), type="l", ylab="F(x)")
> abline(h=c(0, 1), v=0, col="blue", lty=3)

No.14745　Re: 指数分布の確率密度関数　　【統計の子猫】　2011/06/08(Wed) 07:35

青木先生，

お返事ありがとうございます。
先生のお返事のあと，少し自分で確率と確率密度の違いを調べてみました。
下記の理解で正しいでしょうか？

二項分布やポアソン分布のような離散的な分布では，確率変数が「ある値をとる確率」が求められる。
指数分布や正規分布のような連続的な分布の場合は，確率変数が「ある値をとる確率」が求められるのではなく，「ある範囲の値をとる確率」はその範囲で確率密度を積分することにより求められる。これは無限の精度で点を処理した場合，離散型とは異なり，「特定の値」を取る確率はゼロになってしまうので，「各点に与えられた確率」に基づいて確率分布を定義することは不可能になってしまいます。そこで，微小であったとしても，ある範囲を設定する必要がある。

ところで，連続的な分布の式は，“確率密度関数”と呼ばれていますが，二項分布やポアソン分布などの離散的な分布の式は，なんと呼べばよいでしょうか？積分すると1になるので，やはり“確率密度関数”でしょうか？それとも離散分布の場合は，“確率関数”と呼ぶのでしょうか？

もし離散的な分布に対しても連続的な分布に対しても，確率密度関数と呼ぶ場合，離散的な分布の確率密度関数は，確率変数が「ある値をとる確率」が求められると解釈すればよいでしょうか？

No.14746　Re: 指数分布の確率密度関数　　【青木繁伸】　2011/06/08(Wed) 08:13

離散分布の場合は，f(x) は確率です。