「統計学関連なんでもあり」の過去ログ--- 044

No.14654　α係数について　　【はなこ】　2011/05/19(Thu) 10:43

α係数についてご指導ください。
手元にテストデータ（正誤）があるのですが，Rでα係数を計算すると絶対値1を超えてしまいます。
どういう場合にこのようなことになるのでしょうか？またこれはデータとしては使い物にならないのでしょうか？
よろしくお願いします。

No.14656　Re: α係数について　　【青木繁伸】　2011/05/19(Thu) 14:02

逆転項目があるんじゃないですか?
定義式を見ればそのようになることの理由がわかると思います。以下に例を示しておきます。
> x
   x1 x2 x3 x4
1   3  4 10 13
2   8  8  7 10
3   4  6 10 10
4   7  3  9 10
5   7  8  9  7
6   2  2 12 11
7   7  6 10  9
8   6  6  7  7
9   5  4 11 10
10  2  2 14 14

> alpha(x)
alpha = -3.98788 # 「絶対値が 1 を超える」とは，こういうことでしょう?

> round(cor(x), 3)
       x1     x2     x3     x4 # 相関係数行列 x1, x2 は x3, x4 と逆転
x1  1.000  0.737 -0.791 -0.715
x2  0.737  1.000 -0.749 -0.688
x3 -0.791 -0.749  1.000  0.702
x4 -0.715 -0.688  0.702  1.000

No.14658　Re: α係数について　　【はなこ】　2011/05/19(Thu) 18:00

青木先生，お返事ありがとうございます。
外国人7名に対して，日本語のリスニングテストを課しています。マーク形式のもので，全部で10問あります。正解不正解を01で表現したものが下記のデータです。
  q1 q2 q3 q4 q5 q6 q7 q8 q9 q10
1  0  0  1  0  0  1  1  0  0   0
2  1  0  0  1  0  1  0  0  0   0
3  0  0  1  0  0  0  0  1  0   1
4  1  0  0  0  1  0  1  0  1   0
5  0  1  0  1  0  0  1  0  1   0
6  1  0  0  0  1  0  1  0  1   1
7  0  0  1  0  1  1  0  0  0   1
この結果がつぎのものです。
> library(psy)
> cronbach(x)
（中略）
$alpha
[1] -3.796296
アンケートではありませんので，逆転項目はないはずです。
これは使い物になりませんでしょうか？
よろしくお願いいたします。

No.14659　Re: α係数について　　【青木繁伸】　2011/05/19(Thu) 18:58

アンケートでなくても逆転項目はあります。

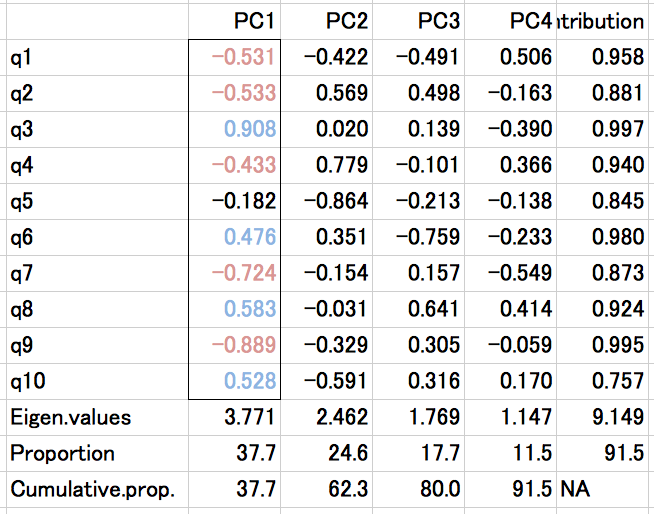
q1～q10 を主成分分析（変数>ケース数なので R の prcomp を使う。また，同様の理由で因子分析ができない）を行っても，4つの主成分が出てきます。例えばそのうちの第 1 主成分についてみれば，q1, q2, q4, q7, q9 と q3, q6, q8, q10 は符号が異なるので逆の意味を持つことがわかります。これはそれぞれが互いに逆転項目であることを意味します。第2主成分以降についても同じです。いずれにせよ，q1 ～ q10 を同格のものとして扱うことができないので，単純に q1 ～ q10 の得点を足し算して合計点を出した場合には，各得点が打ち消しあって合計点の分散が，それぞれの得点の分散の和よりも小さくなるということになります。そしてそれがまさにαがマイナスの値になるということなのです。（なお，αが -1 ～ 1 の範囲の値を取ると思っているなら，それは間違いです。計算上は -1 より小さい値になることもあります。）

結論としては，今回のデータの限りでは，q1 ～ q10 の単純な合計点で評価するのはまずいと言うことです。つまり，内的整合性はないといいうこと。

q1 ～ q10 がどのような因子構造であるか（どのような質問グループに分けられるか，つまり，どのような合計点が意味を持つか）は，もっとたくさんのデータを取って因子分析なりを行う必要があるでしょう。

No.14660　Re: α係数について　　【はなこ】　2011/05/19(Thu) 19:20

青木先生，
とても丁寧なそしてわかりやすい説明を頂き，すっきりとしました。
ありがとうございました。