「統計学関連なんでもあり」の過去ログ--- 044

No.14111　E(xバー―5)^2＝１/４　　【みた】　2011/01/05(Wed) 23:59

E(xバー―5)^2　　が　1/4
になると書いてあったのですが何故こうなるのですか？

μ＝5，　σ^2＝4，　の正規母集団より大きさn=16の無作為標本を抽出とありました。

No.14114　Re: E(xバー―5)^2＝1/4　　【青木繁伸】　2011/01/06(Thu) 01:15

わからなくても差し支えないでしょう。

No.14121　Re: E(xバー―5)^2＝1/4　　【みた】　2011/01/06(Thu) 22:06

E(xバー―5)^2　　が　1/4
になると書いてあったのですがどうやって解けばいいのですか？

μ＝5，　σ^2＝4，　の正規母集団より大きさn=16の無作為標本を抽出とありました。

基本的な問題ですみません。

No.14124　Re: E(xバー―5)^2＝1/4　　【青木繁伸】　2011/01/06(Thu) 23:18

N(5, 2^2) から n=16 の標本抽出を行うと，標本平均の平均は 5，標準偏差（正確に言えば標準誤差）は sqrt(2^2/16)=1/2（標本平均の性質）。
個々の標本平均から平均を引いて(x.bar-5)，二乗して (x.bar-5)^2，平均をとる E[ (x.bar-5)^2 ] というのは，分散の定義そのもの。分散は標準偏差の二乗だから (1/2)^2=1/4 になる。
こういうの，分かっても分からなくても，どうということはない。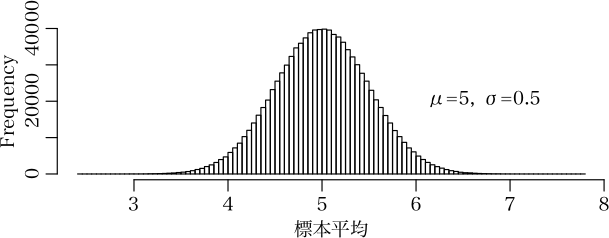

No.14128　Re: E(xバー―5)^2＝1/4　　【みた】　2011/01/07(Fri) 12:58

わかりました！ありがとうございます！

No.14134　Re: E(xバー―5)^2＝1/4　　【みた】　2011/01/07(Fri) 23:09

（すみません。続きです）
「μ＝5，　σ^2＝4，　の正規母集団より大きさn=16の無作為標本を抽出で」
E(x_1―5)^2　　が　4となっていました。

これらは
E(x_1―5)^2→x_1...x_nの分散＝σ^2=4

E(x_bar―5)^2→標本平均の分散＝σ^2/n＝1/4

というので合っていますか？すみません。

No.14135　Re: E(xバー―5)^2＝1/4　　【青木繁伸】　2011/01/08(Sat) 09:41

あっていないと思うのですか？

No.14136　Re: E(xバー―5)^2＝1/4　　【みた】　2011/01/08(Sat) 18:46

間違っていたらいやなので。ありがとうございます。