No.13995 Re: non-selectiveになる場合のGLM 【GLM躓き者】 2010/12/18(Sat) 03:56
大変,失礼しました。
以下のような生データです。weight preyA preyB sum
10 10 0 10
15 12 0 12
19 20 1 21
21 21 2 23
25 30 4 34
30 32 7 39
32 29 10 39
33 31 15 46
35 28 21 49
38 27 24 51
41 30 25 55
42 29 27 56
44 30 28 58
50 32 30 62
餌はカウントデータで,family=binomialを当てています。> model <- glm(cbind(preyA, sum-preyA) ~ weight, family=binomial, data=data01)
> summary(model)
Call:
glm(formula = cbind(preyA, sum - preyA) ~ weight, family = binomial,
data = data01)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6861 -0.4585 0.3545 0.9439 2.0676
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.68739 0.45945 8.026 1.01e-15 ***
weight -0.08300 0.01183 -7.018 2.26e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 75.874 on 13 degrees of freedom
Residual deviance: 15.882 on 12 degrees of freedom
AIC: 65.908
グラフは以下のように当てはまりがよくありません。
おそらく二項分布(binomial)を指定しているのがまずいと思うのですが,代わりに何を指定すればいいかわかりません。
よろしくお願いします。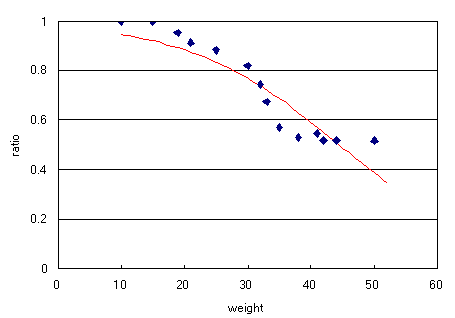
No.13999 Re: non-selectiveになる場合のGLM 【青木繁伸】 2010/12/18(Sat) 11:19
ただ単に似ているからと言うだけでロジスティック曲線を当てはめてみると以下のようになった。> d <- read.table("data01.R", header=TRUE)
> d$y <- d$preyA/d$sum
> ans <- nls(y ~ 0.5/(1+a*exp(-b*weight))+c, d, start=list(a=-0.5, b=-0.06, c=0.5))
> p <- ans$m$getPar()
> (a <- p[1])
a
0.000284451
> (b <- p[2])
b
-0.262103
> (c <- p[3])
c
0.4885675
> x <- seq(0, 60, length=1000)
> y <- 0.5/(1+a*exp(-b*x))+c
> plot(x, y, type="l")
> points(d$weight, d$y, pch=19, col="maroon2", xpd=TRUE)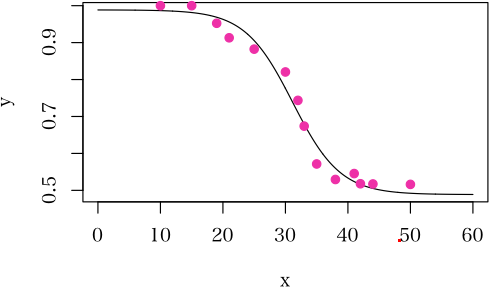
No.14001 Re: non-selectiveになる場合のGLM 【竹澤】 2010/12/20(Mon) 09:04
ノンパラメトリック一般化線形回帰を使うと,例えば以下のようになります。function() {
library(mgcv)
weight <- c(10,15,19,21,25,30,32,33,35,38,41,42,44,50)
preyA <- c(10,12,20,21,30,32,29,31,28,27,30,29,30,32)
preyB <- c(0,0,1,2,4,7,10,15,21,24,25,27,28,30)
sum <- c(10,12,21,23,34,39,39,46,49,51,55,56,58,62)
gam123 <- gam(cbind(preyA, preyB)~s(weight), family=binomial)
print(summary(gam123))
ey <- predict(gam123, type="response")
plot(weight, preyA/sum, ylim=c(0.4,1.1))
lines(weight, ey)
}回帰曲線は,正規分布を仮定してロジスティック曲線をあてはめた場合とほとんど違いません。しかし,信頼区間などにはかなりの違いが現れるだろうと思います。
No.14005 Re: non-selectiveになる場合のGLM 【知ったかぶり】 2010/12/20(Mon) 16:31
link関数に手を加えれば,
>“ 1 または 0.5 に近づく漸近線”
となるようにすることができます.glm()のlink関数は,自分で定義できるらしいのですが,よくわからないので,optim()を使用.LL2 <- function(a){ # 対数尤度関数を定義
lb <- 1 / (1 + exp(a[3])) # preyAの比率の下限
q <- lb / (1 + exp( - (a[1] + a[2] * weight))) + (1 - lb)
sum(lchoose(sum, preyA) + preyA * log(q) + (sum - preyA) * log(1 - q))
}
model2 <- optim(c(1, -0.1, -0.1), LL2, control=list(fnscale=-1)) # 対数尤度を最大化するパラメータの推定
pa2 <- model2$par # パラメータ推定値
-2 * model2$value + 2 * length(pa2) # AIC
xx <- seq(5, 55, 1)
plot(weight, preyA / sum, ylim=c(0, 1), xlim=c(0, 55))
lines(xx, (1 / (1 + exp(pa2[3]))) / (1 + exp( - (pa2[1] + pa2[2] * xx))) + (1 - (1 / (1 + exp(pa2[3])))), col=2)パラメータの数は1つ増えますが,AICは普通にlogitリンクを使った場合より小さくなります.

