No.13632 分散分析における平均平方の意味 【さみだれ】 2010/10/19(Tue) 10:42
文系の者です。初歩的な質問でお恥ずかしいのですが,お知恵を拝借できれば幸いです。
分散分析でF値を算出する際に用いる平均平方(群間および群内)の意味が理解できません。
平方和の分割で群間の効果と群内の効果(散らばり)に分けるという部分はわかるのですが,その後それらを自由度で割って平均平方を算出する部分で,完全に意味を見失います。「自由度一つ分の散らばり」とは,いったい何のことでしょうか。
特に混乱に拍車をかけるのが,これらを「群間分散」「群内分散」と表現している教科書があることです。この「分散」とは,いったい<何の>分散を指しているのでしょうか?
私
が想像するに,平均平方=分散とは,標本データの分散ではなく,母集団における平均の標準誤差(の2乗)を指しているのではないかと思えるのですが,この
理解で正しいでしょうか?例えば,群<内>平均平方=群内分散というのは,各群に属すデータの分布から推定される各群の母集団平均の標準誤差の2乗である
−これはなんとなく正しいように思えます。しかし,これと同じ考え方に従うと,群<間>平均平方=群間分散というのが<何の>平均の標準誤差(の2乗)を
意味しているのかがわからず,この考え方も間違っているのかな,と思えてきます。
結局,私が知りたいことは,「群内平均平方,および群間平均平方とは,いったい<何の>分散を指しているのか」という問題であると思われます。何卒お知恵を拝借できれば幸甚です。
No.13635 Re: 分散分析における平均平方の意味 【青木繁伸】 2010/10/19(Tue) 12:07
> 私が想像するに,平均平方=分散とは,標本データの分散ではなく,母集団における平均の標準誤差(の2乗)を指しているのではないかと思えるのですが,この理解で正しいでしょうか?
あ
なたは間違っています。また,「想像する」意味などありません。ちゃんとした参考書を見れば済むことです。そこには,群間分散(級間分散と書いている参考
書もあります),群内分散(おなじく級内分散とも)の説明もちゃんとありますし,全分散が群間分散と群内分散に分解されることが示されているでしょう。
「自由度一つ分のちらばり」などと説明している参考書があるのでしょうか。まあ,間違いではないけど,混乱を招く余計な説明ですね。ある変数の変動(分散分析では平方和とも呼ぶ)を自由度(n-1)で割ったら不偏分散(おなじく平均平方)ですよね。
3個のデータの和が15になったとき,平均値は15/3 = 5/1 = 5 で,「平均値というのは,データ1個あたりのデータの値」ということですけど,そんな風にいうとかえって変でしょう?
> この「分散」とは,いったい<何の>分散を指しているのでしょうか
全分散を二つの部分に分解した分散ですよ。群間のデータのバラツキ(平均値の差によるバラツキ)と群内でのデータのバラツキ。
添付図の注
矢印の長さはそれぞれの分散の大きさを表すものではない
群内分散が2つの矢印で描かれているが,2つに分かれているわけではない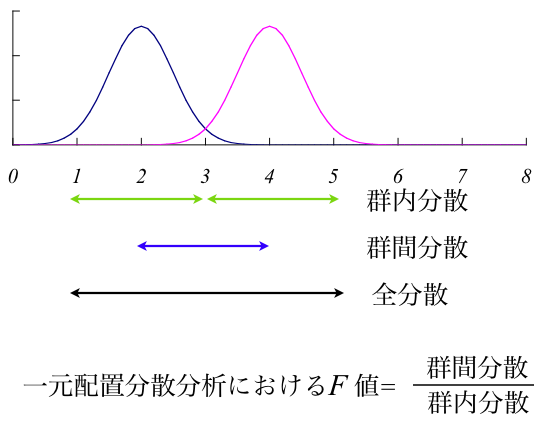
No.13636 Re: 分散分析における平均平方の意味 【さみだれ】 2010/10/19(Tue) 12:57
青木先生,早速のご指導ありがとうございます!
ただ,説明を拝見してさらにわからなくなってしまいました。
>> この「分散」とは,いったい<何の>分散を指しているのでしょうか
>
> 全分散を二つの部分に分解した分散ですよ。群間のデータのバラツキ(平均値の差によるバラツキ)と群内でのデータのバラツキ。
と
ありますが,これは偏差平方和の分割の話ではないでしょうか(全てのデータのバラツキ=群間のデータのバラツキ+群内でのデータのバラツキ)。一番わから
ないのは,平均平方の算出の際に,群間と群内で異なる自由度で割ってしまうということで,その結果全分散を「分解」した状態にはならないのではないかとい
うことです(全分散≠群間分散+群内分散)。
物わかりが大変悪く,申し訳なく思っています。ご指導よろしくお願い申し上げます。
No.13639 Re: 分散分析における平均平方の意味 【知ったかぶり】 2010/10/19(Tue) 16:19
以下の資料がわかりやすいのでは.
http://elsur.jpn.org/resource/anova.pdf
ポイントは,平方和同様,自由度も分割される,ということでしょうか.
No.13640 Re: 分散分析における平均平方の意味 【青木繁伸】 2010/10/19(Tue) 18:24
そりゃね,偏差平方和が分割されるんですよ間違いない。
だれも,全分散=群間分散+群内分散 とはいっていないでしょ?
で,それを自由度で割ったものが平均平方(不偏分散)ですよ。
群間変動(群間偏差平方和)と群内変動(群内偏差平方和)は単純に比較できません。
平方和はサンプルサイズが大きくなると(自由度も大きくなりますけど),それにつれて大きくなりますからね。で,自由度で割って(平均平方になるわけです)を比較するんです。
No.13641 Re: 分散分析における平均平方の意味 【kai】 2010/10/20(Wed) 10:31
結局,私が知りたいことは,「群内平均平方,および群間平均平方とは,いったい<何の>分散を指しているのか」という問題であると思われます。何卒お知恵を拝借できれば幸甚です。
平均平方と分散は厳密には異なるものです.
平均平方の中で分散と呼べるのが誤差の平均平方のみです.
平均平方は母分散の推定値である分散成分にある係数を乗じた状態で合成された値になっています.誤差の平均平方のみ,群内の分散成分のみから構成されているので分散と呼べますが,残りは違います.
例えば今回例にあがっているような一元配置の分散分析では,各群で繰り返し数が等しいとした場合,群間の平均平方は群間の分散成分に繰り返し数を乗じた値と群内の分散成分を足した値になります.
No.13642 Re: 分散分析における平均平方の意味 【さみだれ】 2010/10/20(Wed) 17:25
知ったかぶりさん,青木先生,kaiさん,本当にありがとうございます!
青木先生の「平均平方
(不偏分散)ですよ」というお言葉で,これまでの個人的なわだかまりのかなりの部分が解消されました。平均平方は自由度を用いて算出するので,母集団の
「何か」を表現しているのだろうとは想像していたのですが,不偏分散(母分散の推定値)だったのですね。(特に「群内」の場合は→下記Kaiさんへの返答
参照)
そして,知ったかぶりさんの紹介して下さった文書は感動もののすばらしさですね!これほど包括的,詳細,そして文学部系人間にもわ
かるように(←ここが重要)分散分析を説明してくれた教科書はついぞ拝見したことがありません。特に重要だと感じたのが「つまり,MSAはσ2Aの不偏推
定量ではなく,σ2Aとσ2Errorの両方を反映する統計量なのである。」という部分です。これがわかった瞬間に,これまで理解が困難だった平均平方の
意味,そしてF値の意味がわかりました。
Kaiさんの「一元配置の分散分析では,各群で繰り返し数が等しいとした場合,群間の平均平方は
群間の分散成分に繰り返し数を乗じた値と群内の分散成分を足した値になります」というコメントについては,まだ完全に理解できた自信がありません。是非確
認させていただきたいのですが,これは基本的には,上記の「MSAはσ2Aの不偏推定量ではなく,σ2Aとσ2Errorの両方を反映する統計量なのであ
る。」と同じ内容だと理解してよろしいでしょうか。そして「群間の分散成分に繰り返し数を乗じた値」=「σ2Aの不偏推定量」と理解してよろしいでしょう
か。ただ,この場合の「繰り返し数」とは何を指しますか。サンプルサイズ,群の数,あるいはその他の数でしょうか。大変お手数ですが,もしご教示いただけ
れば幸いです。
数十年来の疑問が解ける瞬間が近づいている気がして,個人的に非常にエキサイトしております。皆様本当にありがとうございます!
No.13652 Re: 分散分析における平均平方の意味 【kai】 2010/10/21(Thu) 13:00
私の説明した内容は,日本規格協会の[新編統計的方法]という本(著者は森口繁一)の8章で詳しく説明していま
す.この本は統計の基本的な事項についてきちんと記述しているバイブルのような本ですので是非参考にしてください.この本には二元配置の場合の分散成分に
ついても記述があります.また,特筆すべきは50年前に書かれた本であるのに変量効果についての説明があることです.
「MSAはσ2Aの不偏推定量ではなく,σ2Aとσ2Errorの両方を反映する統計量なのである。」 → そのとおりです.
ちなみに,繰り返し数は各水準で取得したデータの数のことです.1つの水準につき5つデータを取得していた場合,MSA=σ2Error+5*σ2A となります.
No.13654 Re: 分散分析における平均平方の意味 【さみだれ】 2010/10/21(Thu) 16:42
kaiさん,丁寧なご教示ありがとうございました。大変よくわかりました。
ご紹介の本,図書館で借りて読んでみます。
皆さんのおかげで,これまでの疑問が一気に解けました。
本当にうれしいです。ありがとうございました!
追記:
と
ころで,今回少々気になったのが,この分散分析のロジックを理解する上で極めて重要な点(=平均平方には何が含まれ,また母集団の何を表現したものである
のか)が,多くの文系向け(特に心理・教育系)の教科書では正確に説明されていないことです。私の手元には都合12冊のこうした教科書があります(どれを
読んでも理解できないので,買いまくりました)。これらを改めて確認してみると,上記の点に正確かつ文系人間にわかるように文章で(←これ重要)言及して
いるものは極めて少数だということがわかりました(特に,群間平均平方の意味が比較的丁寧に解説してあるのは1冊のみでした)。中には,自由度で割ること
が,まるで標本分散の算出時のように,あたかもサンプルサイズの調整をしているだけのように書いてある教科書もありました。
「わかりやすい」と銘打った教科書は多いですが,こうした極めて重要な事実の説明を回避したり,ごまかしたりしてしまうと,結局は「文系の私には,はなから統計を正確に理解することは無理なのだ。」という無力感を与えてしまうことにつながりかねません。
こ
こで手をさしのべてくれた皆さんや,紹介していただいた資料のように,文系人間にはわかりにくいことを,きちんとわかる言語で伝えてくれる教科書がもっと
多く出版されればうれしいと心より祈っています。(もちろん,教科書執筆の大変さは身にしみてわかっているつもりです...)
Thanks very much,
No.13655 Re: 分散分析における平均平方の意味 【kai】 2010/10/22(Fri) 09:05
分散成分については言及している本は確かに少ないですね.
永田先生の書かれた[入門実験計画法]は初級〜中級者向けに詳細に分散分析の解析方法を説明していますし,巻末のQ&Aがかなり実用的で役に立ちます.
統計解析に関する本では永田靖先生と芳賀敏郎先生の本は論理的に正確な表現で書かれており,かつ内容に飛躍がない(←重要)のでお勧めです.
● 「統計学関連なんでもあり」の過去ログ--- 044 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る

