「統計学関連なんでもあり」の過去ログ--- 043

No.13386　点双列相関について　　【しば】　2010/09/10(Fri) 17:10

被験者が判断したデータの評定値（名義尺度，0：ありふれた，1：特別な）と評定者が評価したデータの評価値（順位尺度：0～3で値が大きいほど特別）の相関を求めるよう言われました。
この場合，使用するのは点双列相関だとおもうのですが
(1) 計算は「被験者の評定値」と「実験者の評価値」の相関係数を求めればよいのでしょうか？
(2) 被験者が判断した評定値と評定者の評価値のそれぞれで，傾向は同じ（どちらも特別と判断された数が多い）なのですが，相関係数が非常に低くなってしまいます。点双列相関を用いないほうがよいデータということなのでしょうか？（図がそのデータです。値はデータ数です）

よろしくお願いいたします。

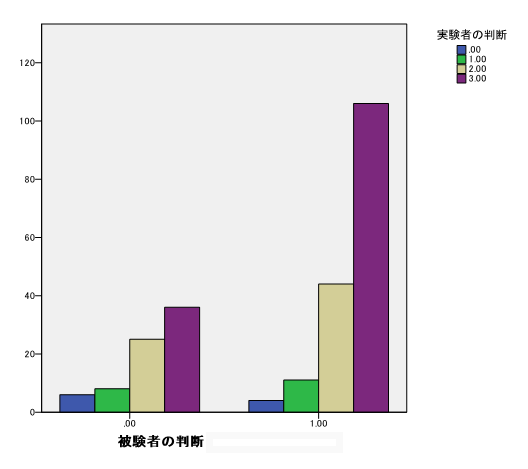
No.13387　Re: 点双列相関について　　【青木繁伸】　2010/09/10(Fri) 18:23

提示された図は，二変数の関係を示すには不適切ですね。関係を読めません。
ここに添付する図もあまり適切ではないけど，これをみれば計算された相関係数が低いのも納得できるでしょう。データポイントが散らばって描かれていますが，そのあたりの一箇所に全部のデータが重なっているんだと頭の中で想像してみてください。要するに，クロス集計表の8個のセルの中央にそのセルに集計されているだけのデータがあるということと同じです。

まあ，原因の一部は「点双列相関を用いないほうがよいデータ」ということでしょう。点双列相関係数というのは相関係数（ピアソンの積率相関係数）なのですから，0/1の二値データならよい（間隔尺度として扱って良い）のですが，順位尺度はだめ（0,1,2,3という数値を使って計算してはだめ）。計算するなら，順位相関係数を使わないと。もっとも，順位相関係数を計算しても，同じでしょう。一番水準の低い名義尺度とみなしてクラメール係数をもとめても，ほぼ同じ。

要するにこのデータには相関がないので，別の何かを計算すれば相関が高いことになるようなものではないです。

No.13396　Re: 点双列相関について　　【しば】　2010/09/11(Sat) 21:17

＞青木先生

丁寧な解説を頂き，ありがとうございます。
大変勉強になりました。
ご指摘いただいたとおり，順位相関係数を求めてもやはり低い値でした。
この場合，相関がないのはデータが8つの領域にほぼ均等に散らばっているためである，という表現で正しいのでしょうか？

No.13397　Re: 点双列相関について　　【青木繁伸】　2010/09/12(Sun) 08:11

> 相関がないのはデータが8つの領域にほぼ均等に散らばっているためである

均等に散らばってはいないでしょう。
「被験者の評定値」別に「実験者の評価値」の割合（％）を求めて見てください。良く似ているでしょう。つまり，被検者の評定にかかわらず，実験者の評価値はほぼ同じ（つまり，両者は関係が弱い）そういうことです。いきなり相関を計算するのではなく，基礎的な集計をして，その結果をよく吟味する必要があります。

No.13398　Re: 点双列相関について　　【ひの】　2010/09/12(Sun) 11:44

>この場合，相関がないのはデータが8つの領域にほぼ均等に散らばっているためである，という表現で正しいのでしょうか？

　何が原因で何が結果かというのは難しい問題ですが，「データのせい」にするのはおかしいでしょう。元々の現象に相関がないからデータの解析結果もそうなった，と考えるのでなければなんのためのデータ解析なのか分かりません。

No.13406　Re: 点双列相関について　　【しば】　2010/09/14(Tue) 15:11

＞青木先生
データの形をみたり，基礎的な集計を行ってから，という観点が抜けておりました。今後，気をつけたいと思います。
ご指導ありがとうございます。

＞ひの先生
ご指導，ありがとうございます。
確かに，現象が先にあっての解析結果と考えるのが妥当ですね。
基礎的なことを念頭におかず，お恥ずかしい限りです。
大変勉強になりました。ありがとうございます。