「統計学関連なんでもあり」の過去ログ--- 043

No.13007　相関係数の求め方　　【空】　2010/07/08(Thu) 00:02

本の例題です。

問題
8人の生徒の数学xと理科yの成績の対(x,y)を調べて次の表を得た。
数学の成績と理科の成績の相関係数を求めよ。

質問1
u=(x-50)/10という式はどこから出てきたものでしょうか？

質問2
u=(x-50)/10の式の-50と10はどこからの数字になるのでしょうか？

xの平均を計算しても500/8で62.5になってしまいます。
xを階級値としても階級値の幅は一定ではないため算出方法がわかりません。
u=(x-50)/10は，ui=(xi-a)/cからxi=cui+aからのものではないかとも思ったのですが
階級値の幅が一定ではないということ。
本にはa=度数の一番大きな階級値とあります。
しかし，この表では度数は8人の生徒一人一人の成績が書かれてあるため，
度数はそれぞれ1になると思ったのです。
そうすると，u=(x-50)/10という出所がわかりません。

宜しくお願い致します。

No.13008　Re: 相関係数の求め方　　【ひの】　2010/07/08(Thu) 01:03

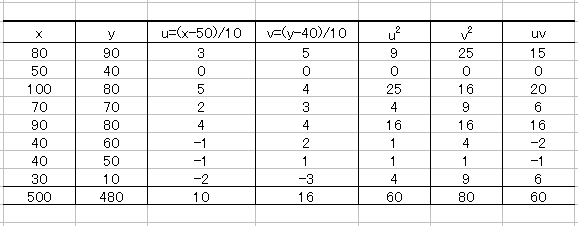
出題者の意図はよくわかりませんが。元のデータを適当に一次変換しても求まる相関係数の値は変わりません。エクセル等で，x,yの相関係数と，u,vの相関係数をそれぞれ求めてみてください。全く同じ値になるはずです。

したがって，

u=(x-50)/10

の式の 50，10という数字は実数なら何でも構いません（0で割るのだけはダメ）。

たとえば

u=(x-0)/1

とすれば u = x になります。

　平方や積の計算を手計算で行うときに，線形変換で元のデータの値を簡単な計算しやすい数値にするためにこのようなことを行っているのです。相関係数を手計算で求めていた太古の昔の計算技法です。パソコンで計算するならこのようなことは全く必要ありません。

No.13010　Re: 相関係数の求め方　　【韮澤】　2010/07/08(Thu) 08:22

なんとなくですが，成績x,yは，学校等で使われる，いわゆる偏差値のデータで，そこから，標準偏差u,vに変換したいのではないでしょうか?
uvの意味は分かりませんが

No.13013　Re: 相関係数の求め方　　【青木繁伸】　2010/07/08(Thu) 11:19

> u=(x-50)/10という式はどこから出てきたものでしょうか？

元の x を使って計算するのは暗算ではちょっと面倒なので，一桁くらいの簡単な整数にできればよいなあということでしょう。例えば，u₁ = (x - 60) / 10 でもかまいません。このとき，u₁ = 2, -1, 4, 1, 3, -2, -2, -3 となり，その平均値は 2 / 8 = 0.25 になります。u₁ の平均値と x の平均値の間にも，u₁ = (x - 60) / 10 が成り立ちますので，この式を x についてといて，x = u₁ * 10 + 60 になります。この式によって，x の平均値は u₁ の平均値から，0.25 * 10 + 60 = 62.5 となり，x から直接求めた平均値 62.5 と同じになります。添付図のようになります（黒がデータ，赤が平均）。

No.13014　Re: 相関係数の求め方　　【空】　2010/07/08(Thu) 12:01

わかりました！

ひのさん
数字は0以外なら何でも良いということから適当に数字をあてはめてみました。
u=(x-50)/10　を　u=(x-20)/5　としました。
本の例題の答えと，自分の数字の答えが一致しました。
エクセルを使ったほうが簡単なのかもしれませんが，レポート提出とテストがあるので
手書きと電卓で頑張ります；；

韮澤さん
偏差値のデータである場合もあるということ，心得ておきます！

青木さん
u=(x-50)/10　を　u=(x-60)/10　と定めた時　0.25*10+60=62.5　
u=(x-50)/10　を　u=(x-20)/10　と定めた時　8.5*5+20=62.5　
xの平均=(x1 + x2 +.....)/N=62.5
と，同じになりました！
データまで，わざわざ作成してくださってありがとうございます。

みなさん，ありがとうございました。
是非また宜しくお願い致します。