「統計学関連なんでもあり」の過去ログ--- 043

No.12887　ロジスティック曲線　　【川島】　2010/06/22(Tue) 17:07

はじめて投稿させてもらいます。統計学を独学でしている者ですが，ロジスティック曲線について質問があります。元のデーターをロジット変換して，それを確率値にして，ロジスティック曲線を作成したいのですが，株価のチャートのようになってしまうのですが，どうしたら滑らかな曲線になるのかよいのか教えてください。ご返答のほど宜しくお願いします。

No.12888　Re: ロジスティック曲線　　【青木繁伸】　2010/06/22(Tue) 18:25

> 元のデーターをロジット変換して，それを確率値にして，ロジスティック曲線を作成したい

どのようなデータなんでしょうか？

普通，ロジスティック曲線に当てはめるデータというのは，独立変数は数値データ，従属変数は 0/1 の二値データで，それに対して GLM で回帰式を求める。
> df <- data.frame( # データフレーム
+ x1 = c(62.3, 50.0, 52.5, 57.5, 49.5, 51.7, 54.4, 57.2, 52.4, 46.4, 33.6, 38.1),
+ x2 = c(55.8, 46.7, 48.9, 52.1, 49.5, 51.3, 55.6, 53.0, 52.7, 51.5, 48.7, 44.6),
+ y  = c(1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0))
> df
     x1   x2 y
1  62.3 55.8 1
2  50.0 46.7 0
3  52.5 48.9 0
4  57.5 52.1 1
5  49.5 49.5 0
6  51.7 51.3 0
7  54.4 55.6 1
8  57.2 53.0 0
9  52.4 52.7 1
10 46.4 51.5 1
11 33.6 48.7 1
12 38.1 44.6 0
> ans <- glm(y~x1+x2, family=binomial(link="logit"), data=df)
> summary(ans)

Call:
glm(formula = y ~ x1 + x2, family = binomial(link = "logit"), 
    data = df)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-1.36168  -0.20814   0.01881   0.41217   1.71507  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept) -66.1574    44.9378  -1.472    0.141
x1           -0.3952     0.2544  -1.553    0.120
x2            1.6828     1.0594   1.588    0.112

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 16.6355  on 11  degrees of freedom
Residual deviance:  6.8964  on  9  degrees of freedom
AIC: 12.896

Number of Fisher Scoring iterations: 7

> plot(ans$linear.predictor, ans$fitted.values, pch=1)
> lp <-  seq(-7, 7, length=1000)
> lines(lp, 1/(1+exp(-lp)))
> points(ans$linear.predictor, df$y, pch=19)
もしそういうことでなければ，データ例（実際のものでなくてもよい）と分析例を示してみてください。

No.12903　Re: ロジスティック曲線　　【川島】　2010/06/24(Thu) 16:33

ご回答ありがとうございます。よく分からないのでデータを投稿させていただきます。ちなみにこのデーターはある木材の製品の合否についてのデーターです。やる手順は以下のようになります。P(ロジット変換)→loge{P/(1-P)}＝L　＊ここでのeはロジット変換の際の自然対数の底は約2.72と本に掲載されてました。
これを回帰分析して確率値に戻す。
L→loge[exp(L)/{1+exp(L)}]=p　＊ここでのexp(L)はe^Lとのことです。
最後にこのpをロジスティック曲線にする。ちなみにデーターのロジット変換と確率値に戻すのは自分でやりました。ご回答のほどよろしくお願いします。
 比重 繊維密度 色素量 合否     合否 ロジット変換値      確率値
0.815    0.295     53    0 -0.06674   -0.027186893 0.214329123
0.851    0.333     53    1  0.91688    4.793788410 0.431010490
0.831    0.261     44    0  0.19284    0.103823776 0.228561085
0.833    0.243    160    1  0.77473    1.494523548 0.354998276
0.854    0.210     17    1  0.49017    0.417815410 0.262055296
0.844    0.280     33    0  0.50682    0.446592028 0.265041747
0.834    0.253     58    0  0.31567    0.200456097 0.239003439
0.827    0.241     64    0  0.14237    0.072141958 0.225123664
0.833    0.228     28    0  0.07604    0.035761761 0.221171730
0.839    0.291     48    0  0.48758    0.413507826 0.261606698
0.830    0.256     30    0  0.08528    0.040515398 0.221688313
0.836    0.325     76    1  0.64239    0.780620626 0.298079560
0.819    0.196     48    0 -0.25142   -0.087309168 0.207799028
0.843    0.253     29    0  0.39190    0.280066555 0.247533023
0.839    0.293    111    1  0.80761    1.824175261 0.374252569
0.828    0.270     48    0  0.16257    0.084360228 0.226449884
0.832    0.275     92    1  0.49375    0.423841750 0.262682220
0.856    0.270     46    1  0.84059    2.291495321 0.394714987
0.850    0.230    213    1  1.42342   -1.460909324 0.081780313
0.844    0.265     53    1  0.56767    0.570616403 0.277684564
管理人注：名前が違っていました（不要ですので，削除しました）。確率を確立とする変換ミスがありました（修正しました）。フォーマットを整えました。数式も，括弧を補うなどしないと，訳の分からない計算式になります（修正しました。今回は，よく知られている計算式なので括弧のつけ忘れで変な計算をする恐れがないだけです）。

No.12905　Re: ロジスティック曲線　　【青木繁伸】　2010/06/24(Thu) 17:12

4列目の，0／1 データの「合否」から，5 列目の合否はどうやって計算するのですか。
P(ロジット変換)→loge{P/(1-P)}＝L　の P は表のどれですか？どれでもないのですか？

なにをどうやったのか，これだけの説明では何も分かりません。

> データーのロジット変換と確率値に戻すのは自分でやりました

エクセルでやったのかと思いますけど，「ここでのeはロジット変換の際の自然対数の底は約2.72と本に掲載されてました」などとやらなくても，LN というのが自然対数を求める関数です（ちなみに，LOG は常用対数関数）。逆変換は，EXP という関数です。

先の説明のように，木材の比重，繊維密度，色素量とその合否(0/1)が分かっていれば，いわゆるロジスティック回帰を行って，予測式を求め，その予測式を用いて，先に示したような図を描くのですけどね？

No.12906　Re: ロジスティック曲線　　【青木繁伸】　2010/06/24(Thu) 17:41

比重，繊維密度，色素量を全部使うと完全な予測ができるようなので，比重と繊維密度だけを使った予測例。
横軸の linear.predictor を求めるのに，

(Intercept)  -142.99
比重          164.94
繊維密度       17.44

の部分のが使われるのです。すなわち，
linear.predictor = -142.99+164.94×比重+17.44×繊維密度
そして，そのようなlinear.predictor を持つ木材が合になる確率が
1/(1+exp(-linear.predictor))
となるのです。

> ans <- glm(合否 ~ 比重+繊維密度, data=d, family=binomial)
> summary(ans)

Call:
glm(formula = 合否 ~ 比重 + 繊維密度, family = binomial, 
    data = d)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.6665  -0.6188  -0.2017   0.7514   1.7815  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  -142.99      63.86  -2.239   0.0251 *
比重          164.94      74.84   2.204   0.0275 *
繊維密度       17.44      20.12   0.867   0.3861  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 27.526  on 19  degrees of freedom
Residual deviance: 18.384  on 17  degrees of freedom
AIC: 24.384

Number of Fisher Scoring iterations: 5

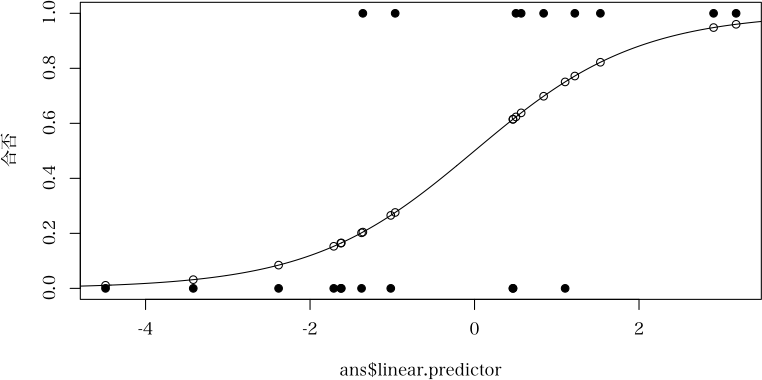
> plot(ans$linear.predictor, 合否, pch=19)
> points(ans$linear.predictor, ans$fitted.values)
> lp <-  seq(-7, 7, length=1000)
> lines(lp, 1/(1+exp(-lp)))

linear.predictor と合になる確率（Prob）を表にしておきます。

    比重 繊維密度 色素量 合否 linear.predictor  Prob
1  0.815    0.295     53    0           -3.420 0.032
2  0.851    0.333     53    1            3.181 0.960
3  0.831    0.261     44    0           -1.374 0.202
4  0.833    0.243    160    1           -1.358 0.205
5  0.854    0.210     17    1            1.530 0.822
6  0.844    0.280     33    0            1.102 0.751
7  0.834    0.253     58    0           -1.019 0.265
8  0.827    0.241     64    0           -2.382 0.085
9  0.833    0.228     28    0           -1.619 0.165
10 0.839    0.291     48    0            0.469 0.615
11 0.830    0.256     30    0           -1.626 0.164
12 0.836    0.325     76    1            0.567 0.638
13 0.819    0.196     48    0           -4.487 0.011
14 0.843    0.253     29    0            0.466 0.614
15 0.839    0.293    111    1            0.504 0.623
16 0.828    0.270     48    0           -1.712 0.153
17 0.832    0.275     92    1           -0.965 0.276
18 0.856    0.270     46    1            2.907 0.948
19 0.850    0.230    213    1            1.219 0.772
20 0.844    0.265     53    1            0.840 0.698