「統計学関連なんでもあり」の過去ログ--- 043

No.12880　被験者内の回帰分析？　　【ann】　2010/06/21(Mon) 17:31

はじめまして。annと申します。

早速本題ですが，下記のように，xが1要因6水準の量的な独立変数，yが従属変数（量的変数），sはサンプルとなっているデータの場合，x，yが共に量的変数なので，回帰分析ができると思うのですが，実際にはどのようにすればいいのでしょうか？

――――――――――――――
　　x1　x2　x3　x4　x5　x6
――――――――――――――
s1　y11 y12 y13 y14 y15 y16
s2　y21 y22 y23 y24 y25 y26
s3　y31 y32 y33 y34 y35 y36
s4　y41 y42 y43 y44 y45 y46
：
si　yi1 yi2 yi3 yi4 yi5 yi6
――――――――――――――

ある論文と同じ分析をしたいのですが，論文にはOLSで頑健標準誤差（robust standard error）に基づき検定をしたとしか書いてなくて困っています。

分析法について書いてある本だけでも教えて頂けたら幸いです。

No.12883　Re: 被験者内の回帰分析？　　【波音】　2010/06/22(Tue) 09:49

>　xが1要因6水準の量的な独立変数
>　x，yが共に量的変数なので，回帰分析ができる

この場合，xは量的なデータ（連続型のデータ）ではなく，質的なデータ（カテゴリカル型のデータ）です。yが連続型でxが6つの水準を持つカテゴリカル型変数ですから，1要因の分散分析です。

なお一般線形モデルの枠組みでは，分散分析はダミー変数を用いた回帰分析に等しいといえます。

No.12885　Re: 被験者内の回帰分析？　　【ひの】　2010/06/22(Tue) 12:37

>この場合，xは量的なデータ（連続型のデータ）ではなく，質的なデータ（カテゴリカル型のデータ）です。

質問者が量的データと書いているのに，質的なデータであると決めつける根拠は？
普通に考えると順序尺度以上だと思いますけれど。

No.12886　Re: 被験者内の回帰分析？　　【kai】　2010/06/22(Tue) 14:35

ロバスト回帰などで色々引っかかるとは思いますが．

以下のページの［講義ノートと補遺：後半］のファイルに頑健標準誤差について色々説明があります．
http://www.eco.osakafu-u.ac.jp/~kano/LightNEasy.php?page=econometrics

No.12890　Re: 被験者内の回帰分析？　　【波音】　2010/06/22(Tue) 23:08

> 質問者が量的データと書いているのに，質的なデータであると決めつける根拠は？

まず「1要因6水準の量的な独立変数」というデータは"ない"でしょう。連続型の変数が水準（levels）を持つということはないわけですから(^_^;)

質問者さんが提示されているデータセット（形式）は列方向に水準を置いてありますが，データフレームの形式に置き換えれば添付図のようになるはずです（添付図はx1とx2しか書いてありませんが）。

変数xは6つの水準を持っているということから，xは連続型ではなくカテゴリカル型だと考えるのが一般的かと思ったわけです。そう考えれば，提示されたデータセットも要因の水準（x1からx6まで）が列方向に置かれたものであろうな，と察したわけです。

私の早とちりならお騒がせ致しました。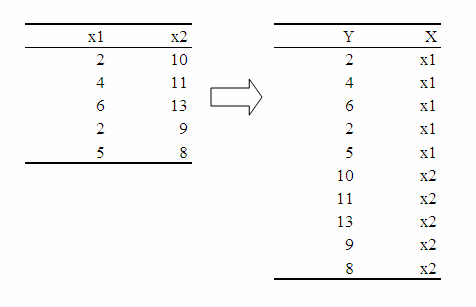

No.12891　Re: 被験者内の回帰分析？　　【ひの】　2010/06/23(Wed) 07:59

>変数xは6つの水準を持っているということから，xは連続型ではなくカテゴリカル型だと考えるのが一般的

「連続型でないならばカテゴリカル型」というのは飛躍していると思います。間隔尺度，順序尺度の可能性もあります。

No.12896　Re: 被験者内の回帰分析？　　【ann】　2010/06/23(Wed) 16:47

私の説明不足で申し訳ありません。
どうやら要因と水準という言葉を使用したのが間違っていたみたいですね。

どういうデータか具体的に説明すると，これは独裁者ゲームに第3者の制裁オプションを追加した第3者制裁ゲームと呼ばれるゲームのデータです（Fehr, E., & Fischbacher, U. (2004). Third-party punishment and social norms. Evolution and Human Behavior, 25, 63-87.）。　

このゲームでは3人のプレーヤー，A，B，Cがポイントをやりとりします。ゲーム開始時，Aは100点，Bは0点，Cは50点持っていて，まず，Aは100点の内，何点をBに譲るか（50，40，…0点）決定します（譲渡量）。これが上記の独立変数になります。次に，AがBに譲った点数に応じて，Cは50点の内，何点を使ってAの点数を減らすか決定します（制裁量）。これが従属変数になります。ただし，この時，CはAの全ての譲り方（50，40，…0点）に対して，制裁量を決定するため，下記のようなデータになると思われます。

――――――――――
　50 40 30 20 10　0
――――――――――
1　1　3　8 11 14 17
2　0　2　6 13 15 18
3　0　1　9 10 12 12
:　:　:　:　:　:　:
――――――――――

このデータに対して，Fehr & Fischbacher(2004)では譲渡量を独立変数，制裁量を従属変数とした回帰分析をしていて，それと同じ分析をしたいので質問しました。

元論文では以下のように書いてあり，

OLS regression of punishment on the variable (50-transfer) confirms this result, yielding a highly significant (P < .001) slope coefficient of .28 while the constant is close to zero (-0.45) and not significant (P = .230).

これに脚注で以下のように付け加えられてあります。

Our significance tests are based on robust standard errors that take into account the fact that a given individual's punishment choices are dependent observations, whereas across individuals the punishment choices represent independent observations.