「統計学関連なんでもあり」の過去ログ--- 043

No.12704　続　信頼区間について　　【Hara_da 】　2010/05/24(Mon) 15:29

すみません。以下についてもご教示いただければ幸いです。
（前の質問と紛らわしいので，スレッドを変えました）

The formula used to calculate 95% confidence interval can be misleading if there are less than around 60 observations. This is because the method is based on the assumption that the true standard deviation is known. In practice, as with the mean the population standard deviation has to be estimated by the sample standard deviation. With smaller samples this has a noticeable impact, making the true 95% confidence interval a little wider. To compensate for this the multiplier of 1.96 from the Normal distribution is replaced by a slightly bigger value.

ここで言う式というのは，母集団既知での95%CI算出式のようです。
上記で標本の大きさが60といのが，どういった根拠か不思議だったのですが，t分布表で，α = 0.05となる係数が1.96を上回る点が60のようなので，そう考えると，上で言わんとしていることは，「真の標準偏差が未知の場合には不偏分散を利用するが，このとき，標本サイズが十分大きければ，そのまま正規分布を仮定しても，結果に大差はない。しかし，標本サイズが小さくなると，区間幅が広くなるので，係数を大きく補正する。つまり，t分布を仮定する」というようなことでしょうか。

ついでに，上で係数1.96をmultiplierと言っていますが，この日本語訳もご存知でしたらご教示いただければ助かります（もしかして，乗数かなとも思うのですが）。

No.12705　Re: 続　信頼区間について　　【青木繁伸】　2010/05/24(Mon) 17:47

> というようなことでしょうか。

そういうことでしょう。

> multiplier

テクニカルタームというほどのものでないので，倍数とか乗数とかなんでもよいでしょう。

No.12707　Re: 続　信頼区間について　　【Hara_da】　2010/05/24(Mon) 20:02

青木先生，ご回答くださりありがとうございます。大変助かりました。大変恐縮ですが，いま少し（？）ご教示願えれば助かります。ちょっと多いのですが，まとめて掲示いたします。

(1) If either of the outcomes is infrequent, then its proportion is close to 0, the 95% confidence interval calculated by this method may include values of less than 0 or greater than 1.(ここで，この方法とは， SEとしてsqrt(p(1-p)/n)を使う方法のこと)。
上記で，pが0に近ければCIの間隔は狭くなりそうに思えるのですが，この文の後に，If the number of observations for the infrequent outcome is below 5, the exact method should be used.　とあることからすると，これはあくまで，nが非常に少ない場合に限定した話ということなのでしょうか。

(2) If one of the two outcomes does not occur at all, the lower sample proportion is equal to zero.
ここで，lower sample proportionといのはsqrt(pq)/n)の，例えば，p < qとして，pのことを言っているのだろうと思うのですが，次の質問との関連で見れば，下側限界のことを言っている，あるいは，その両方？，という気もするのですが。この点について，意見を伺いたいのですが。

(3)上の文に続いて，However, even if a particular outcome is not observed in a sample it does not mean that it can never occur.
標本に観測されないこと，not = 発生確率　0で，このような考えに立ってrule of 3を用い，その場合，下限値を0とするとのことですが，これについて何も理由が説明されていません。p+z^2/2n ±sqrt(p(1-p)/n+(z/2n)^2)/(1+z^2/n)がp = 0だと0になるからかと考えたいところだったのですが，続いて，上限は3/nにすると書かれていました。そうなると，どうも何故そのように限界値を設定できるのか分かりません。これについても，ご教示いただければ，幸いです。

(4) 仮説検定で，「差があり」という仮説から検定を行うと，因子を有する群に差があるという検定結果になってしまう」と説明されておりました。この理由がよく分からないのですが，命題が曖昧なために，棄却限界が設定できず，検定者の考え一つで，有意差ありとできる，もしくは，標本サイズを大きくすれば，意味があるなしにかかわらず有意差が出るから，ということかと考察したのですが，考え方としておかしいな点があるでしょうか。

質問数が非常に多くなってしまい恐縮ですが，何卒宜しくお願いします。

No.12709　Re: 続　信頼区間について　　【青木繁伸】　2010/05/24(Mon) 21:43

(1) 要するに，その方法では信頼限界が 0 以下とか 1 以上になることがあるということを言っているだけで，n がそんなに小さくなくてもそういうことは起こりえます。添付図参照。特に，"number of observations for the infrequent outcome" が 5 以下の時には正確な方法を使えといっていますが，いつだって正確な方法を使え場良いだけの話です（前の質問で n が小さいときには正確な方法すなわち t 分布を使う方法を使えというのも，いつも正確な方法を使えば良いだけの話）。

(2) 事象が観察されなかった（裏を返せば，他方の事象が100％観察された）というような場合には，小さい方の事象が起きた確率は 0 ということ。つまり，硬貨を 10 回投げて，表が0回（表が10回）出た場合，小さい方の確率は共に 0（表が 0，その逆の場合は裏が 0）ということ。

(3) しかし，観察された確率が 0 でも，そのような事象が全く起こらないことは意味しない，ということ。硬貨を 10 回投げて，表が 0 回出た場合でも，表は絶対でないということは意味しないということ。
「rule of 3を用い，その場合，下限値を0とする」は，下限値は 0 以下はあり得ない。上限値は 1 以上はあり得ない。だって，割合はそういう定義ですから。

(4) 「差がある」という仮定をする場合，どれくらいの差があるかを明示して論を進めなければならないのだが，差が 1 なのか，1.2345 なのか 3.432 なのか，無数にあり対処しがたい。「命題が曖昧なために，棄却限界が設定できず」ということはありません。特定の値を仮定すれば，ある事象が起きる確率だって，明確に計算できます。
「検定者の考え一つで，有意差ありとできる，もしくは，標本サイズを大きくすれば，意味があるなしにかかわらず有意差が出るから」というのは，無関係です。

統計学のお勉強なのか，英語のお勉強なのか明確にした方が良いでしょう。日本語で書かれた統計学のしっかりした教科書をまずお読みになると宜しいかと。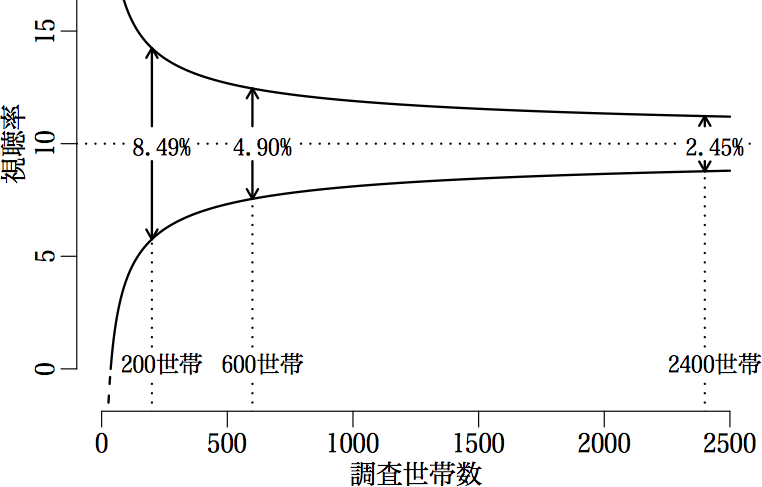

No.12711　Re: 続　信頼区間について　　【Hara_da】　2010/05/24(Mon) 22:28

図解入りで分かりやすくご教示いただき感謝申し上げます。

>統計学のお勉強なのか，英語のお勉強なのか明確にした方が良いでしょう。日本語で書かれた統計学のしっかりした教科書をまずお読みになると宜しいかと。

全く仰るとおりではありますが，故あって両方同時に進めざるを得ない状況にあり，一人で格闘しておりましたが，この掲示板を発見し，ご助力をお願いしている次第です。日本語の書も都度読んではいるのですが，細かい，定義的な点で詳しい説明がなく，どうもしっくり理解できない点が残る（誤解している心配もある）ので，ここで自分の疑問を解消させていただいております・

(4) ですが，，「因子を有する群に差があるという検定結果になってしまう」とい言っているのは，考えられる差は無数にあり得るので，これを恣意的に設定できれば，検定を厳しくすることも，ゆるくすることもできるので，そうなると言っているのでしょうか。

お忙しいのに何度もお聞きし，恐縮ですが，ご教示の程宜しくお願いいたします。

No.12712　Re: 続　信頼区間について　　【青木繁伸】　2010/05/24(Mon) 22:42

帰無仮説は，「差は0である」つまり「等しい」とするのが普通ですが，「差はδである」というようにすることもできます（そのようなオプションを設けているソフトは多いです）。しかし，δを適当に決めるのでは，仰るようにどのような結果も出せるし，δ=0.5 では有意ではなかったので，δ=0.55 にしたら有意になったなどということになるわけで，止めどなくなってしまうと言うことです。

No.12713　Re: 続　信頼区間について　　【Hara_da】　2010/05/25(Tue) 01:03

青木先生，遅い時間であるにもかかわらず，ご回答くださり大変感謝しております。
お陰さまで，非常に助かりました。