No.12453　指数分布で並ぶ点に操作を加えると　　【こう】　2010/04/14(Wed) 15:04

隣り合う各点の間隔εが，指数分布になるように，直線状に点を並べます。
つまり，点の位置をX1 , X2 , X3 , ・・・ , Xn ,　Xn+1 ・・・　として，εn = Xn+1 - Xn とすると，ε1 , ε2 , ε3 ・・・　の分布が　指数分布となります。

この点に対して，次の操作を加えたとき，各点の間隔の分布はどうなりますか？

1）ランダムに＋a ，−a　のいづれかを加える。操作後の点の位置は，例えば，X1+a , X2+a , X3-a , X4+a , X5-a , ・・・・　のようになります。

2）順番に＋a ，−a　を加える。操作後の点の位置は，X1+a , X2-a , X3+a , X4-a , X5+a , ・・・・　のようになります。

初歩的な質問かも知れませんが，よろしくお願いします。
No.12455　Re: 指数分布で並ぶ点に操作を加えると　　【青木繁伸】　2010/04/14(Wed) 17:44

実際に差をとって（ろうとしてみて）よく考察すればおわかりと思います。
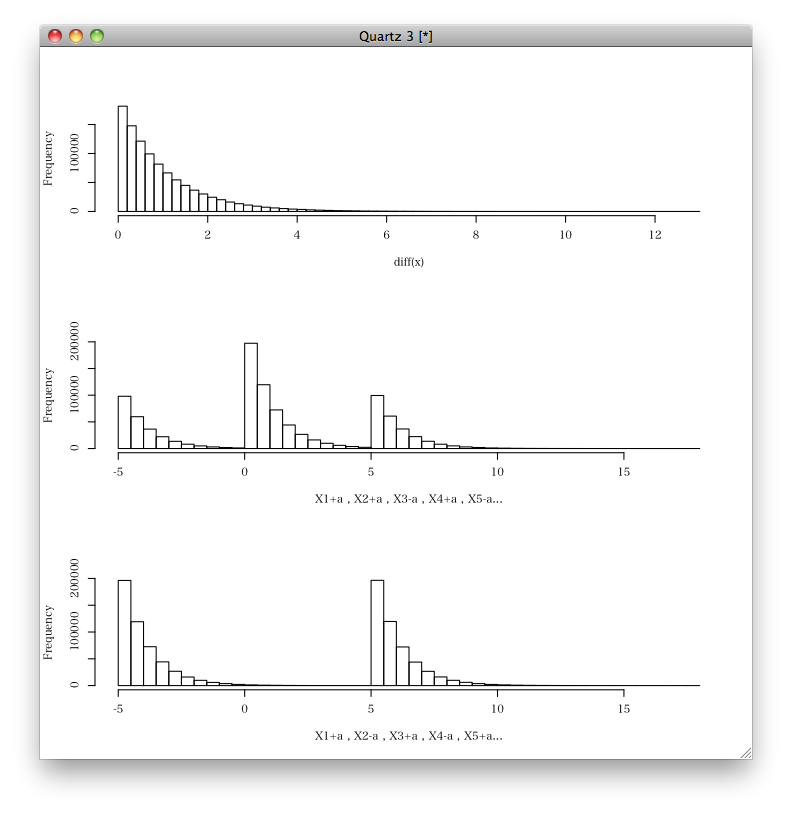
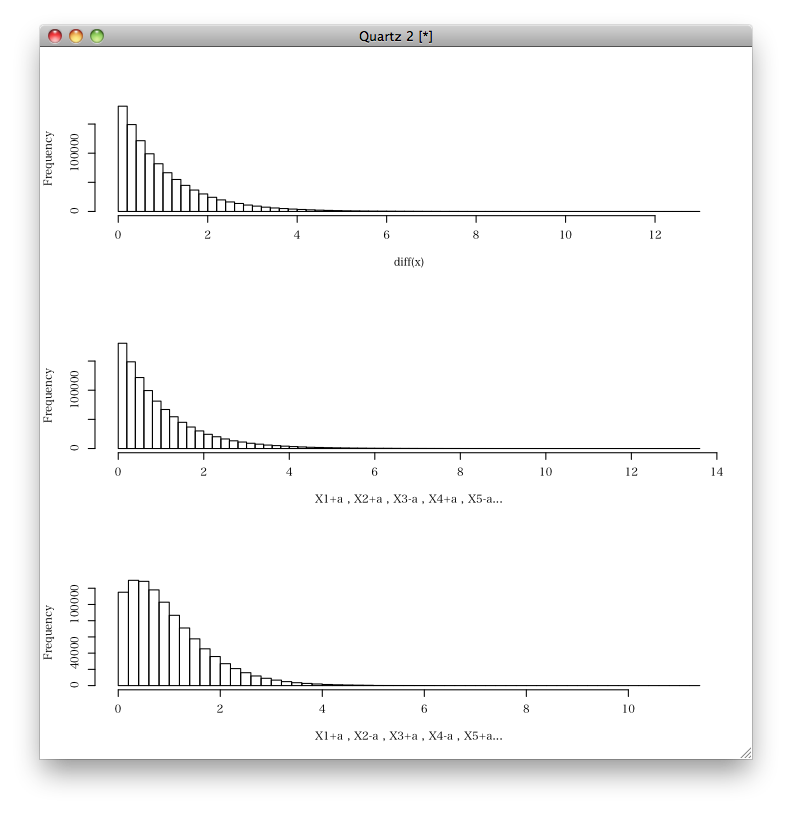
ランダムならば，差は，本来の差のものと，本来の差+2aのものと，本来の差-2a のものという3種類生じるわけで，元の指数分布とそれを ±2a 平行移動したものの分布の和でしょう。
順番に±aを加えるならば，本来の差+2aのものと，本来の差-2a のものという2種類生じるわけで，指数分布を ±2a 平行移動したものの分布の和でしょう。
layout(matrix(1:3, 3))
n <- 1000000
x <- cumsum(rexp(n))
hist(diff(x), nclass=50, main="")
a <- 2.5 # 大きくした方が分かりやすいので
y2 <- x+sample(c(-a, a), n, replace=TRUE)
hist(diff(y2), nclass=50, xlab="X1+a , X2+a , X3-a , X4+a , X5-a...", main="")
y3 <- x+c(-a, a)
hist(diff(y3), nclass=50, xlab="X1+a , X2-a , X3+a , X4-a , X5+a...", main="")

No.12457　Re: 指数分布で並ぶ点に操作を加えると　　【こう】　2010/04/14(Wed) 23:22

早々のご回答ありがとうございます。
もし，操作によって，各点の順序の入れ替わりがなければ，ご回答の通り分布の和になると思うのですが，順序が入れ替わる場合はどうなるでしょうか。
例えば，X1 , X2 , X3 の順番だったのが，操作によって，X1 , X3 , X2 になった場合は，考える各点間の間隔としては，X3-X1 , X2-X3 としたいのですが。
間隔εに対して，操作で加える a の絶対値が大きい場合に，入れ替わりが起きます。

説明が足りなくてすみません。
よろしくお願いします。
No.12459　Re: 指数分布で並ぶ点に操作を加えると　　【青木繁伸】　2010/04/15(Thu) 08:28

ランダムな場合には確率的にデータが入れ替わるだけですから，全体の分布は変わらないでしょう。規則的な場合には指数分布ではなくなるようですね。
layout(matrix(1:3, 3))
n <- 1000000
x <- cumsum(rexp(n))
hist(diff(x), nclass=50, main="")
a <- 2.5 # 大きくした方が分かりやすいので
y2 <- x+sample(c(-a, a), n, replace=TRUE)
hist(diff(sort(y2)), nclass=50, xlab="X1+a , X2+a , X3-a , X4+a , X5-a...", main="")
y3 <- x+c(-a, a)
hist(diff(sort(y3)), nclass=50, xlab="X1+a , X2-a , X3+a , X4-a , X5+a...", main="")

No.12468　Re: 指数分布で並ぶ点に操作を加えると　　【こう】　2010/04/16(Fri) 18:58

ありがとうございます。

たびたびの質問で恐縮なのですが，この分布，式で表すことできないでしょうか。

よろしくお願いします。
No.12469　Re: 指数分布で並ぶ点に操作を加えると　　【青木繁伸】　2010/04/16(Fri) 20:51

> この分布，式で表すことできないでしょうか。

そもそも，この問題，どういう背景で出てきたんでしょうか？

学 校で出された課題？実際の現場で浮かび上がったもの？前者なら，答えはあるんでしょうね。後者なら，あるかどうか，私は知りません（前者であっても，私に は分からないのですけど）。後者なら，式で表されなくてもブートストラップなどで実用的な解を求めることは可能でしょう。
No.12473　Re: 指数分布で並ぶ点に操作を加えると　　【こう】　2010/04/17(Sat) 11:12

仕事の中で出てきた，実現象をモデル化して数値解析シミュレーションしている中で浮かび上がった問題です。（詳細は言うことできません。すみません。）

操 作後のCV％が，ランダムの場合には，操作前と変わらず（これは上で示していただいた分布が変わらないことで説明つきますね），規則的な場合には，操作前 よりも小さくなる，という結果が出まして，想定していた結果と逆だったもので，一般的な数式に表すことで説明つかないか，と考え質問させていただきまし た。

ブートストラップ法は，自分で調べてみます。
どうも，ありがとうございました。

● 「統計学関連なんでもあり」の過去ログ--- 043 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る