「統計学関連なんでもあり」の過去ログ--- 043

No.12079　ロジスティック回帰　　【実験まにあ】　2010/02/16(Tue) 16:34

統計学初心者です。
ある大きさから突然能力が高くなる，閾値を推定したいと考えております。

データはX軸が体長で，Y軸はテストの結果(得点)としています。ある体長(X1)から得点が上昇し，前後は横ばいであるという結果を統計的に証明したいと考えています。

JMPを用いてロジスティック回帰モデルにあてはめようとしたのですが，Y軸が連続尺度(得点)ではできないといわれてしまいました。
Y軸が連続尺度のデータで，ロジスティックモデルにあてはめることはできますでしょうか？
また，そのほかにも閾値を推定する良い方法やモデルがありましたらご教授願えないでしょうか？
よろしくお願いします。

No.12085　Re: ロジスティック回帰　　【surg】　2010/02/17(Wed) 08:24

> Y軸が連続尺度のデータで，ロジスティックモデルにあてはめることはできますでしょうか？

そもそも，ロジスティック回帰で閾値など求まらないと思いますが。

> また，そのほかにも閾値を推定する良い方法やモデルがありましたらご教授願えないでしょうか？

データを見てないので何とも言えませんが，例えば閾値を越えると得点が線形に増加するのであれば，閾値の前後で別々の線形モデルをあてはめて，残差の最小二乗和が最小になるような閾値を求めれば良いのでは．

> ある体長(X1)から得点が上昇し，前後は横ばいであるという結果を統計的に証明したいと考えています。

統計学では「証明」はできません．

No.12089　Re: ロジスティック回帰　　【surg】　2010/02/17(Wed) 11:29

Rでやろうとすると，こんな感じでしょうか．

> # 適当なデータ：50までは0，それ以後は1ずつ増加，正規分布で誤差を追加
> data <- data.frame(
+ x = 1:100,
+ y = c(rep(0, 50), 1:50) + rnorm(100)
+ )
> 
> # モデル関数：thrまではa1で一定，thrを超えると1増加するごとにb2増加
> model <- function(x, thr, a1, b2) {
+ sapply(x, function(t) 
+ if(t < thr) a1
+ else b2 * (t - thr) + a1
+ )
+ }
> 
> # 残差平方和
> ssr <- function(p) {
+ sum((data$y - model(data$x, p[1], p[2], p[3])) ^ 2)
+ }
> 
> # 適当な初期値で残差平方和を最小化
> res <- optim(c(0, 0, 0), ssr)
> 
> # 結果。最初の項目が推定された閾値
> res$par
[1] 50.0144809  0.0488099  1.0004176
> 
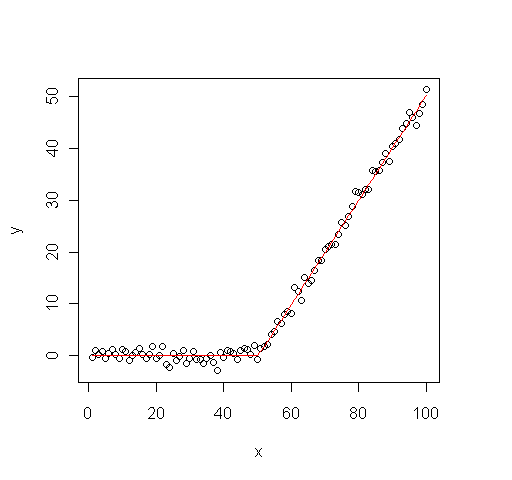
> # 作図
> plot(data)
> lines(1:100, model(1:100, res$par[1], res$par[2], res$par[3]), col=2)

No.12109　Re: ロジスティック回帰　　【実験まにあ】　2010/02/18(Thu) 13:39

ご教授ありがとうございます。
不適切な表現等，失礼いたしました。

ロジスティック曲線では閾値は求められないのですね。変曲点を閾値とすることができないものかと考えてしまっていました。

細かい求め方まで示していただきありがとうございました。
ただ，データについて説明が不足してしまったため，補足させていただきます。

閾値を越えると得点が線形に増加するのでなく，閾値の前後(50以上，50未満)のデータはそれぞれx軸の増加とは相関がない，横ばい傾向を示しました。

X軸のどの値からy軸が増加しているのかを統計的に推定することはできますでしょうか？

No.12110　Re: ロジスティック回帰　　【ひの】　2010/02/18(Thu) 14:11

その図にあるくらい明瞭なデータなら，「統計的に推定」などというまどろっこしい作業は不要なのでは？

No.12111　Re: ロジスティック回帰　　【青木繁伸】　2010/02/18(Thu) 14:41

まあ，閾値の前後では，図ほど明確に区分されていないとしても，surg さんの関数の
 if(t < thr) a1
 else b2 * (t - thr) + a1
を
 if(t < thr) a1
 else a2
と手直しすればよいだけでしょう。つまり，t >= thr でも水平線
> set.seed(111)
> data <- data.frame(x=1:100, y=rep(c(10, 20), each=50)+rnorm(100))
> 
> model <- function(x, thr, a1, a2) {
+   ifelse(x < thr, a1, a2) # sapply(x, function(t) if (t < thr) a1 else a2) と同じ
+ }
> 
> ssr <- function(p) {
+   sum((data$y - model(data$x, p[1], p[2], p[3])) ^ 2)
+ }
> 
> res <- optim(c(40, 0, 0), ssr)
> 
> res$par
[1] 50.566090  9.804163 20.167201
> 
> plot(data)
> lines(c(min(data$x), res$par[1], res$par[1], max(data$x)), res$par[c(2, 2, 3, 3)])

No.12112　Re: ロジスティック回帰　　【実験まにあ】　2010/02/18(Thu) 14:43

お返事ありがとうございます。
確かにそうかもしれませんね。ありがとうございます。
ただ，あまり明瞭でない場合においても推定する方法があるのであればお教え願えないでしょうか？
ちなみに上の図は分かりやすい例を示した物です。実際のデータは下の図になります。

No.12113　Re: ロジスティック回帰　　【実験まにあ】　2010/02/18(Thu) 14:46

青木様
ありがとうございます。コメントが前後してしまい，申し訳ありませんでした。

Rはまだ使ったことがないのですが，この機会に色々といじってみようと思います。
ありがとうございました。