No.11608 Re: 非線形回帰後の線形回帰 【青木繁伸】 2009/12/27(Sun) 22:40
まずは,プログラム
実際にやるときには,1行目(乱数の初期値設定)は削除すること。ただし,いくつかウォーニングは出るでしょう(対処はしているつもりですけど)。
set.seed(11111) # 乱数の初期値実行結果
data <- data.frame( # テストデータ(あなたの手元にあるデータと様相はちがうかもしれないけど,こんな風かな?)
x = c(0.09, 0.09, 0.31, 0.64, 0.93, 1.25, 2.74, 1.51, 1.27, 1.64, 1.95, 2.31, 2.33, 2.56, 2.59),
y = c(0.81, 0.81, 0.43, 1.04, 0.81, 1.66, 4.68, 1.46, 1.09, 2.19, 2.77, 2.47, 3.8, 3.63, 4.24))
pdf("graph%i.pdf", onefile=FALSE, width=500/72, height=400/72) # 2 枚のグラフを描くので,ファイルへ出力
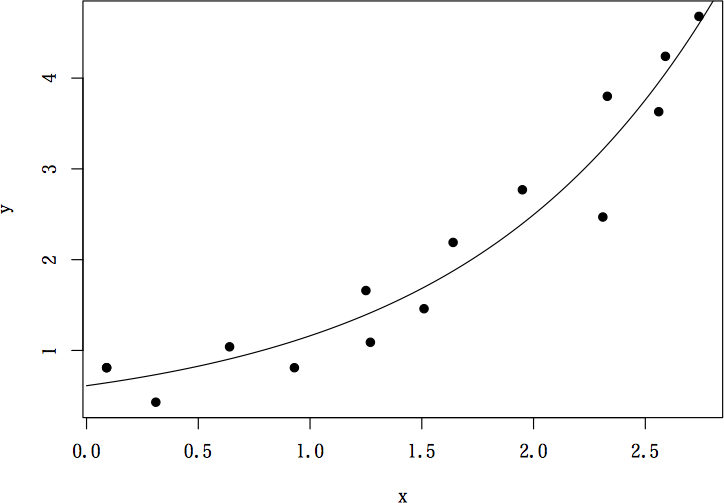
plot(data, pch=19) # データ点のプロット
ans <- nls(y~a1*exp(a2*x)+a3, data, start=list(a1=0.5, a2=0.8, a3=0.1)) # 非線形回帰
summary(ans) # その結果
x2 <- seq(0, 3, length=2000)
lines(x2, predict(ans, newdata=data.frame(x=x2))) # 当てはめ結果の図
n <- nrow(data) # これ以降,ブートストラップ
trial <- 1000 # 繰り替えし数(なるべく多く)
ans <- replicate(trial, # 以下を実行
{
data2 <- data[sample(n, replace=TRUE), ]
try(nls(y~a1*exp(a2*x)+a3, data2, start=list(a1=0.5, a2=0.8, a3=0.1))$m$getPars()[3]) # 任意のパラメータベクトルを抽出(切片といているのはこれ?
})
const <- as.numeric(ans)
const <- const[!is.na(const)] # 推定が成功した場合の結果のみを抽出
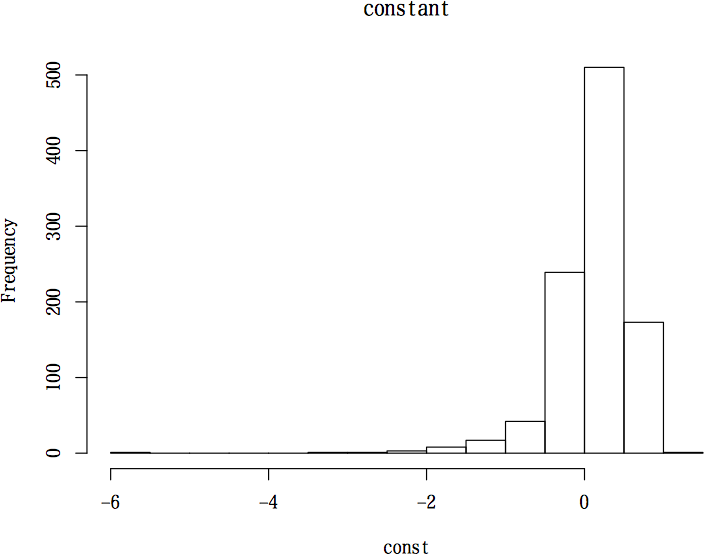
hist(const, main="constant") # ヒストグラムを描いてみる
quantile(const, c(0.025, 0.975)) # 2.5%, 97.5% 点の数値
dev.off()
> set.seed(11111) # 乱数の初期値図
> data <- data.frame( # テストデータ(あなたの手元にあるデータと様相はちがうかもしれないけど,こんな風かな?)
+ x = c(0.09, 0.09, 0.31, 0.64, 0.93, 1.25, 2.74, 1.51, 1.27, 1.64, 1.95, 2.31, 2.33, 2.56, 2.59),
+ y = c(0.81, 0.81, 0.43, 1.04, 0.81, 1.66, 4.68, 1.46, 1.09, 2.19, 2.77, 2.47,
+ 3.8, 3.63, 4.24))
> pdf("graph%i.pdf", onefile=FALSE, width=500/72, height=400/72) # 2 枚のグラフを描くので,ファイルへ出力
> plot(data, pch=19) # データ点のプロット
> ans <- nls(y~a1*exp(a2*x)+a3, data, start=list(a1=0.5, a2=0.8, a3=0.1)) # 非線形回帰
> summary(ans) # その結果
Formula: y ~ a1 * exp(a2 * x) + a3
Parameters:
Estimate Std. Error t value Pr(>|t|)
a1 0.3859 0.2923 1.320 0.21148
a2 0.8860 0.2520 3.515 0.00426 **
a3 0.2256 0.4730 0.477 0.64199
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.377 on 12 degrees of freedom
Number of iterations to convergence: 4
Achieved convergence tolerance: 2.583e-06
> x2 <- seq(0, 3, length=2000)
> lines(x2, predict(ans, newdata=data.frame(x=x2))) # 当てはめ結果の図
> n <- nrow(data) # これ以降,ブートストラップ
> trial <- 1000 # 繰り替えし数(なるべく多く)
> ans <- replicate(trial, # 以下を実行
+ {
+ data2 <- data[sample(n, replace=TRUE), ]
+ try(nls(y~a1*exp(a2*x)+a3, data2, start=list(a1=0.5, a2=0.8, a3=0.1))$m$getPars()[3]) # 任意のパラメータベクトルを抽出(切片といているのはこれ?)
+ })
Error in nls(y ~ a1 * exp(a2 * x) + a3, data2, start = list(a1 = 0.5, :
step 因子 0.000488281 は 0.000976562 の 'minFactor' 以下に縮小しました
Error in nls(y ~ a1 * exp(a2 * x) + a3, data2, start = list(a1 = 0.5, :
step 因子 0.000488281 は 0.000976562 の 'minFactor' 以下に縮小しました
Error in nls(y ~ a1 * exp(a2 * x) + a3, data2, start = list(a1 = 0.5, :
step 因子 0.000488281 は 0.000976562 の 'minFactor' 以下に縮小しました
Error in nls(y ~ a1 * exp(a2 * x) + a3, data2, start = list(a1 = 0.5, :
繰り返し数が最大値 50 を超えました
> const <- as.numeric(ans)
警告メッセージ:
強制変換により NA が生成されました
> const <- const[!is.na(const)] # 推定が成功した場合の結果のみを抽出
> hist(const, main="constant") # ヒストグラムを描いてみる
> quantile(const, c(0.025, 0.975)) # 2.5%, 97.5% 点の数値
2.5% 97.5%
-1.1173381 0.7600651
> dev.off()
quartz
2