No.11503 片側検定?両側検定? 【行動学の研究、統計初心者】 2009/12/13(Sun) 16:56
行動学の実験をしておりまして,T検定の統計手法で悩んでいます。
魚に玉を呈示したときに餌を与えるという学習を条件付けています。条件付けの成立として,「接近行動が呈示前後で有意に増加した」という条件にしているのですが,その際の検定方法についての質問です。
実験は4尾の魚を用いており,玉を呈示する区画(呈示前は何もない)に接近している個体を呈示前と後で各12回計数し,呈示後の接近尾数が有意に増加しているかを「対応のあるt検定」により比較しようと考えています。
この際「片側検定」と「両側検定」のどちらを使えばいいのでしょうか?
増加するという仮説なので「片側検定」かと考えているのですが,条件付けが完成するまでの過程で減少してしまう時もあり「両側検定」のほうが適切なのかとも考えてしまいます。
No.11504 Re: 片側検定?両側検定? 【青木繁伸】 2009/12/13(Sun) 19:57
おっしゃるように,「増加する」という仮説なら「片側検定」
「減少することもある」ということも考えるなら,「両側検定」でよいでしょう。
ただ,「4匹が対象で呈示前と後で各12回繰り返した」ということで,典型的な実験条件(検定の条件)を満たしているかどうか,曖昧なところがあるのではないかと思われ,微妙。
No.11506 Re: 片側検定?両側検定? 【波音】 2009/12/13(Sun) 22:36
統計学の問題というか,行動分析学の問題として:
質問文から察するに「玉が提示されているときに(弁別刺激),ある区画内に進入すると(行動),エサが貰える(結果, 好子の出現)」というものでしょうか。
そうだとすると
> 接近している個体を呈示前と後で各12回計数し,呈示後の接近尾数が有意に増加しているか
という事実から魚が刺激弁別を行っていると判断するのは適切ではないと思われます。
弁別訓練の手続きとして,(1)ランダムに玉を提示し,(2)玉が提示されているとき(弁別刺激SDの下で)エサを与える(強化),一方で玉が提示されていないとき(S⊿の下で)エサは与えない(消去),という手続きを行うべきです。
データで示すなら提示前・提示後というデータではなくて,SDの下における行動の生起頻度とS⊿の下における行動の生起頻度について示すべきでしょう。
No.11508 Re: 片側検定?両側検定? 【行動学の研究,統計初心者】 2009/12/14(Mon) 11:13
ご教示ありがとうございます。
非常に参考になりました。
補足いたしますと,4尾が対象な
のですが,これは単独での実験が不可能であったため4尾を1群としてみて実験を行っており,各個体の違いは無視しております。12回の観察は5秒間隔で1
分間行っており,それぞれの観察の関係は独立したもの(Ex:5秒と55秒は同等の扱い)として考えております。
訓練は「呈示前1分」+「呈示後1分」+「刺激の下での給餌」を1試行としておこなっており,刺激呈示に対する寄付き行動が条件付けられるまで繰り返し行いました。
呈示前の観察は「弁別刺激が呈示されていないときの行動=S⊿」を指しており,呈示後の観察は「弁別刺激が存在するときの行動=SD」を指しています。
今回は,1群のSDの寄付きがS⊿より有意に増加したときに条件付け完成としたいのですが,やはりt検定は適切でないでしょうか?
適切な方法がありましたら教えていただけないでしょうか?
No.11529 Re: 片側検定?両側検定? 【波音】 2009/12/14(Mon) 23:43
> 12回の観察は5秒間隔で1分間行っており,
つまりデータとしては添付図のような古典的なグラフで表されるようなものですね(縦の分割線より左が玉の提示なし,右が玉の提示あり)。
例
えば,今回の例だと侵入した魚が(玉を提示しているときに){A, B, C}{A, B, D}{A, C, D}{A, B,
C}と単に各フェーズ(5秒ごとの観測)の匹数が同じ3匹でも,Aは4フェーズとも,Bは3フェーズ,Cは2フェーズ,Dは1フェーズです。でもデータと
して得られるのは{3, 3, 3,
3}ということは,明らかに重要な情報を見逃していることになるでしょう。Aは完全に刺激弁別できているが,Dは刺激弁別できていない。
もっとも,単独での実験が不可能だから便宜的に各個体の違いを無視したとしているのでしょうが,,, それで刺激弁別していると主張して納得してくれる人がいるのか疑問に思うところです。
> それぞれの観察の関係は独立したものとして考えております。
観
察者(分析者)が便宜的に独立したものと解釈したとしても,統計学的には明らかに独立したものとはいえないでしょう。この場合は個体から繰り返し観測値を
得ている時間的な自己相関と,空間的な自己相関(隣接した空間から得られたデータは何らかの相関関係を持つ)をもつものといえそうです。
> やはりt検定は適切でないでしょうか?
同じようなデータで「対応ありのt検定」あるいは「独立2標本のt検定」として分析している例を見かけますが,私は形式上のもので実質的な意味はないものだと考えています。
> 適切な方法がありましたら教えていただけないでしょうか?
一般線形混合効果モデルという,いわゆる「対応ありのデータ」に対して適切なモデルがありますが,今回の例だと個体を無視しているのでそれも難しいでしょう。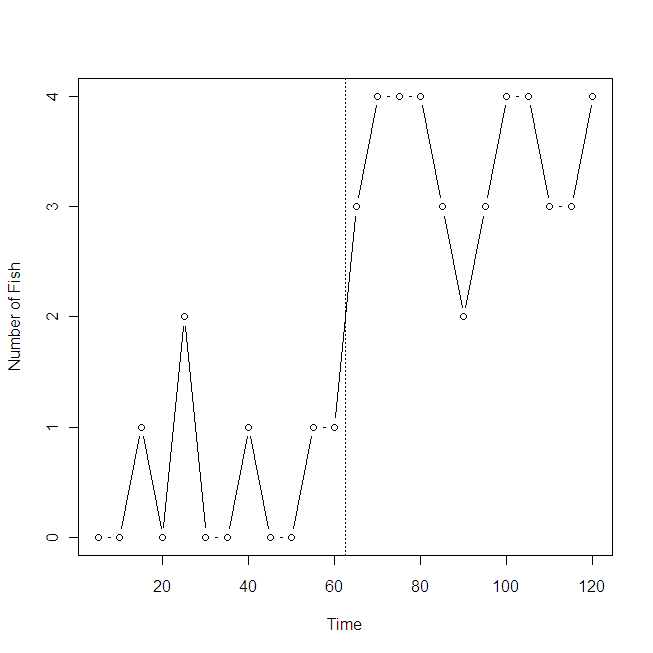
● 「統計学関連なんでもあり」の過去ログ--- 043 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る
