No.11199 Re: loglinear model について 【波音】 2009/11/09(Mon) 09:51
> Fijとuが既知なはずなので，
全平均（切片，定数項）もパラメータの1つとして推定されることになります。観測度数（応答変数）についても，対数線形モデルを解析することで予測するという考え方ですから，どちらも母数が既知であるとはいえないでしょう。
> パラメータの数は「主効果の数＋交互作用（選択肢と意向の組み合わせ分）の数」
基本的な考え方はそうですが，より正確にいえばある説明変数（カテゴリカル型）の水準数が，例えば3つである場合，いずれかの水準がベースラインとして扱われますから，ある主効果について推定するパラメータ数は3-1=2（水準数-1）ということになります。
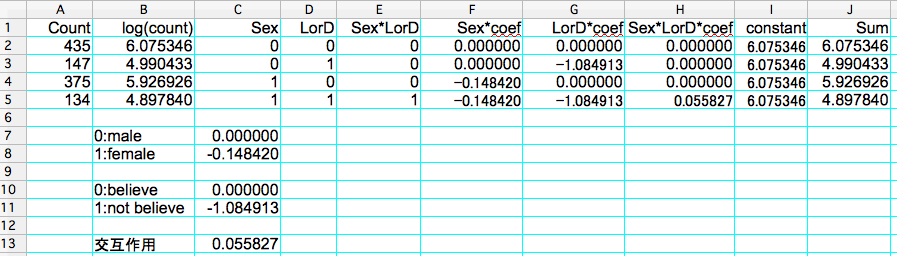
もし複雑な解析で不安ならば，仮のデータを用いて確認してみると良いと思います。渡邉ほか訳『カテゴリカルデータ解析入門』サイエンティスト社（2005）p203の表6.1のデータを参照（以下はRを用いてポアソン回帰モデルを解析した例）。# 観測度数Countと性別Sexと生死観LorDを用意する（R を用いて解析するのか分かりませんが^^;）dummy.coef()を使うと，推定されたパラメータが何であるのか一目瞭然です。Rのglm()という 関数では，デフォルトで第1水準がベースラインとして扱われるので，Sex, maleが0，LorD, beliveが0とされています。交互作用項については，maleとbeliveをベースラインとしているのでこの水準が含まれる組合せは，やはり0と置 かれます。
Count <- c(435, 147, 375, 134)
Sex <- c("male", "male", "female", "female")
LorD <- c("belive", "not belive", "belive", "not belive")
# factor()を使ってカテゴリカル型であることを指定する
# 引数levelsは水準の順位を指定するものである
Sex <- factor(Sex, levels=c("male", "female"))
LorD <- factor(LorD, levels=c("belive", "not belive"))
# glm()を用いてモデル解析
# SexとLorDを*でつないでいるのは，飽和モデルであることを表す
# 引数familyではポアソン分布に従うことを仮定している
model <- glm(Count ~ Sex * LorD, family=poisson)
結局，推定されたパラメータは切片を含めて4つということです。> dummy.coef(model)
Full coefficients are
(Intercept): 6.075346
Sex: male female
0.00000 -0.14842
LorD: belive not belive
0.000000 -1.084913
Sex:LorD: male:belive female:belive male:not belive female:not belive
0.00000000 0.00000000 0.00000000 0.05582722
No.11201 Re: loglinear model について 【TA】 2009/11/09(Mon) 13:49
波音様，ありがとうございます。
> 全平均（切片，定数項）もパラメータの1つとして推定されることになります。
では，対数線形モデルの右辺（u+u1i+u2j+u3ij）が全てパラメータということになるのですね。
> ある主効果について推定するパラメータ数は3-1=2（水準数-1）ということになります。
私 のデータですと，2段階の変数が7つと5段階の変数が1つなので，主効果のパラメータ数だけでも(2-1)*7+(5-1)*1=11，交互作用を含める と・・・。全ての組み合わせまでみる必要はないので，不飽和モデルとして組み合わせが複雑（変数が多い）なものを削ってしまっても良いでしょうか。
パラメータ数など勘違いをしていた点が解け，参考書の説明や式形が少しわかってきました。
Rだとコマンド（glmは一般線形モデルの略ですか？）があるのですね。私はTSPで解こうと考えているのですが，対数尤度関数やパラメータはこちらで設定する必要がありそうです。Rの方がネットなどでプログラムの公開や解説がありますし，やはり使いやすいですか？
No.11203 Re: loglinear model について 【波音】 2009/11/09(Mon) 20:04
> 2段階の変数が7つと5段階の変数が1つ
2つの水準をもつカテゴリカル型の変数が7つ，5つの水準をもつカテゴリカル型の変数が1つ，すべてで8つの説明変数があるということですか。
連続型のみの場合（重回帰分析）でも説明変数が8個もあると，すべての交互作用の解析をしても解釈が難しくなるので，カテゴリカル型ならば仮にパラメータを推定できたにせよどれだけ妥当な解釈ができるか・・・といったところです。
最初からある変数と別のある変数との交互作用について関心があるならば，その項のみをモデルに組み込んでもよいのかもしれません。しかし，8つものカテゴリカル型の変数を説明変数としておいている例をお目にかかったことがないので，確かなことはいえません。
たぶん，実質的に3次以上の交互作用は解釈が難しいので，最初から除外するのが常套手段ではないでしょうか。
---
> glmは一般線形モデルの略ですか？
glm()はGeneralized Linear Modelsの頭文字をとったもので，一般化線形モデルと呼ばれているものです。一般線形モデルはGeneral Linear Modelsですが，Rではlm()で解析することができます。
> Rの方がネットなどでプログラムの公開や解説がありますし，やはり使いやすいですか？
R に用意されているlm()やglm()はモデル解析という考え方（やり方）に対して非常に忠実であると思います。最初にフルモデルを解析して，不要な項を 削除するためにupdate()という関数がありますし，モデル選択の際には他の統計ソフトよりも遥かに便利だと思います。
No.11209 Re: loglinear model について 【TA】 2009/11/10(Tue) 00:06
> 2つの水準をもつカテゴリカル型の変数が7つ，5つの水準をもつカテゴリカル型の変数が1つ，すべてで8つの説明変数があるということですか。
はい，8つ説明変数があります。なので全ての交互作用項，確かに無事推定できたとしても多すぎて何が言いたいのか？となってしまいますね（^^；）
> 最初からある変数と別のある変数との交互作用について関心があるならば，その項のみをモデルに組み込んでもよいのかもしれません。
興味があるのは7つの2水準変数と1つの5水準変数の交互作用なので，ご指摘の通りに組んでみようかと思います。
解釈の話が出たのですが，主効果と交互作用は全基準との差（だと理解している）ので，パラメータの推定値は正であれば組み合わせて選択されやすい，負であれば選択されにくいという解釈でよいのでしょうか？
No.11214 Re: loglinear model について 【青木繁伸】 2009/11/10(Tue) 09:08
> 主効果と交互作用は全基準との差（だと理解している）ので，パラメータの推定値は正であれば組み合わせて選択されやすい，負であれば選択されにくいという解釈でよいのでしょうか
11199 の波音さんの例を，初心に返ってトレースしてみると，添付するように，ln(Count)が Sex，LorD およびその交互作用に対する係数とデータの積和に定数を加えたもの Sum で表されるということですから，それぞれの係数の符号と大きさを眺めてみれば，どのような意味を持っているかわかります。
以下は図として添付（クリックすると拡大）
No.11215 Re: loglinear model について 【TA】 2009/11/10(Tue) 11:38
青木先生，ありがとうございます。
例題について考察し，主効果や交互作用は全基準（全平均）から の（対数をとった）度数の乖離（多い／少ない）の程度であり，各変数の各カテゴリーがクロス表のセルの度数の押し上げ／押し下げに影響しているか，を表し ているのだと解釈しました。（わかりにくい文章ですが・・・）
主効果は，ある変数に関するカテゴリーの集計結果（male△人，female○人でmaleに比べてfemaleは多い／少ない）を表している。
交互作用は，female×not believeである場合，femaleとnot believeの主効果をどの程度緩和（助長）するかを表している。
参考文献に「主効果は一般的に考察・興味の対象とならない」とあったのですが，主効果が集計分析によりわかることそのものだから，対数線形モデルを解くならば交互作用が分析の主眼である，ということなのでしょうか。
変数間の階層関係（充実するオプションの組み合わせ→購買意向決定）が推定結果から判断できないようなので，私が今回行いたい分析方針とは少し離れているようです。
No.11216 Re: loglinear model について 【青木繁伸】 2009/11/10(Tue) 11:58
> 7つのオプションの選択組み合わせ（必要な順に3つ）と購買意向（5段階）の関係を見ることが目的です。
最初から loglinear model といっていたので，スルーしていましたけど，あなたがやりたいことは，多項ロジットモデルではないですか？（購買意向を間隔尺度としてとらえるなら重回帰分析（数量化I類））
つまり，データは，以下のように各被験者ごとに7つのオプションについて必要か不要かと購買意向が得られている。そして，それぞれのオプションが購買意向をどのように決定しているかを知りたいのでは？被験者 オプション1 オプション2 … オプション7 購買意向
あ 1 0 … 1 2
い 0 1 … 1 4
う 0 1 … 0 1
：
No.11217 Re: loglinear model について 【TA】 2009/11/10(Tue) 13:50
青木先生
＞あなたがやりたいことは，多項ロジットモデルではないですか？
対数線形モデルに取り組む前に多項ロジットモデルやオーダードプロビットモデル（購買意向が不完全ながら順序変数なでの）での分析を行いました。
しかし，今回の分析で興味があることは「オプションの組み合わせと購買意向の関係」なので，各オプション単体がもつ購買意向への影響のほかに，複数のオプションが購買意欲へ与える影響を見たいと思っています。
この「オプションの組み合わせと購買意向の関係」を，対数線形モデルの交互作用で表現できるのでは？と思ったのですが，勉強を進めるうちに混乱してきてしまいました。
No.11218 Re: loglinear model について 【波音】 2009/11/10(Tue) 15:23
まず，
> 参考文献に「主効果は一般的に考察・興味の対象とならない」とあった
という言及についてですが，分割表データに対して古典的な独立性の検定（カイ自乗検定）を行うことと，ポアソン回帰モデル（対数線形モデル）において「交互作用項は有意であるかどうか」ということは意味的に同じことをしているわけです。
カ テゴリカル型同士の交互作用が有意であるということは，ある要因の水準と別のある要因の水準の組合せ（例えばmale-beliveという組合せ）におい て極端に大きな値（度数）が得られているということです。*** もちろん，上の例だと交互作用項は有意ではありません。 ***
> 勉強を進めるうちに混乱してきてしまいました。
青木先生がご指摘されているように，応答変数（購買意思）がカテゴリカル型で，その水準数が3つ以上ならば多項ロジットモデルとなるでしょう。
応答変数（目的変数，従属変数）は以下のどれに当てはまるか整理してみると良いかもしれません。説明変数はいずれもカテゴリカル型なので応答変数が以下のいずれかによって，解析しようとするモデルが変わってきます。
連続型 ならば： 分散分析（ダミー変数を用いた重回帰）
カテゴリカル型で水準数が2 ならば： 2値ロジットモデル
カテゴリカル型で水準数が3つ以上 ならば： 名義・順序ロジットモデル
No.11219 Re: loglinear model について 【青木繁伸】 2009/11/10(Tue) 16:19
> 各オプション単体がもつ購買意向への影響のほかに，複数のオプションが購買意欲へ与える影響
多項ロジットモデルなどで，二次，三次…の交互作用項を考えればよいのでは？
loglinear model だけが交互作用を扱うわけではありません。
No.11220 Re: loglinear model について 【にゃんちゅう】 2009/11/10(Tue) 18:13
探索的にどの組み合わせがもっとも反応をよく説明できるかというような問題設定なら，情報量を使ったCATDAP2ですね。
いずれにしても対数線形モデルはかなり使い勝手の悪い手法です。他にもいろいろ手法があるのでデータと目的にあわせて考えてみることです。
No.11222 Re: loglinear model について 【TA】 2009/11/10(Tue) 18:30
波音さん，青木先生
ご指摘ありがとうございます。
応答変数が5水準の順序変数なので，オーダードロジットモデルが適当でしょうか。
＞多項ロジットモデルなどで，二次，三次…の交互作用項を考えればよいのでは？
説明変数が2水準のカテゴリカル変数なので，
V=b1*x1+b2*x2+b3*(x1*x2)
V：評価関数
x1：オプション1を選択する場合1となるダミー変数，b1：オプション1のパラメータ
x2：オプション2を選択する場合1となるダミー変数，b2：オプション2のパラメータ
b3：オプション1とオプション2の交互作用
ということで良いのでしょうか？
非集計モデルならばデータ整備が容易なので，さっそく分析してみたいと思います。
（目的変数，説明変数ともにカテゴリーの選択結果に偏りがあるデータですので，推定結果の信頼性に不安がありますが）
No.11239 Re: loglinear model について 【TA】 2009/11/12(Thu) 13:08
にゃんちゅうさん
ご指摘ありがとうございます。返信が遅くなってしまい申し訳ありませんでした。
＞探索的にどの組み合わせがもっとも反応をよく説明できるかというような問題設定なら，情報量を使ったCATDAP2ですね。
CATDAP2，SPSSやC言語のプログラムがあるようですね？
お手数ですが，勉強するのに適した文献など教えていただけないでしょうか？
No.11242 Re: loglinear model について 【にゃんちゅう】 2009/11/12(Thu) 14:34
坂元慶行(1985) カテゴリカルデータのモデル分析 共立出版
がもっとも詳しいです。
ほかには例えば
情報量統計学 (情報科学講座 A・5・4) (情報科学講座 (A・5・4)) (単行本)
坂元 慶行 (著), 石黒 真木夫 (著), 北川 源四郎 (著) 共立出版
● 「統計学関連なんでもあり」の過去ログ--- 043 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る