No.11053　二項分布におけるp値の範囲推定　　【伊藤】　2009/10/13(Tue) 17:46

初めて質問させていただきます。

不良品の要因解析にて不良品500個の中から100個をサンプリングした。
要因Aで不良になったものが10個あった場合，元の不良品500個中の推定される要因Aの割合範囲の算出方法についてお教えください。。

95%信頼区間
0.1±1.96*((0.1*0.9)/100)^0.5
=0.1±0.059

と計算できると思いますが，このときサンプリング数を増加して行った場合（200個，300個・・・，500個）n数が増えた分信頼区間が狭くなっていき，上記式でn=500とした場合±0.026の範囲となります。
素人の感覚的印象で言えば不良品すべて調べているのだからもっと狭くなっても（範囲は0でも）良いように思います。これは，計算式の適用に問題があるのか，元の不良品500個を母集団と考えているのに問題があるのでしょうか？
No.11056　Re: 二項分布におけるp値の範囲推定　　【青木繁伸】　2009/10/13(Tue) 18:58

有限母集団からの標本サイズ
http://aoki2.si.gunma-u.ac.jp/R/finite.html
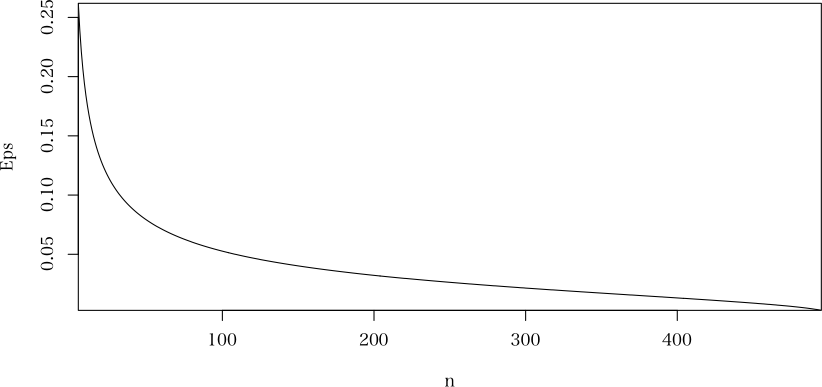
にある，プログラムで，母比率が0.1である母集団500から，標本を5〜495取り出したとき，信頼度0.95での精度（誤差；Eps）を求めてみます。Epsは信頼区間の幅の半分です。
> n <- 5:495
> Eps <- sapply(n, function(n) finite(n=n, N=500, p=0.1, conf.level=0.95)$epsilon)
> plot(n, Eps, type="l", xaxs="i", yaxs="i")
> cbind(n, Eps)
         n         Eps
  [1,]   5 0.261900599
  [2,]   6 0.238836058
  [3,]   7 0.220886134
  [4,]   8 0.206428300
  [5,]   9 0.194424629
  [6,]  10 0.184251989
  [7,]  11 0.175499286
  [8,]  12 0.167856381
　　　　途中省略
[486,] 490 0.003743209
[487,] 491 0.003538984
[488,] 492 0.003384721
[489,] 493 0.003156828
[490,] 494 0.002914067
[491,] 495 0.002652827

図は，クリックすると原寸表示されます。

し かし，あなたが知りたいのは，不良品500個の中の要因Aによる不良割合の信頼区間ではなく，無限母集団における不良割合の信頼区間ではないですか？つま り，500というのは母集団ではなく，取りあえず標本を採るためにとっておいただけのものということではないのですか。500個たまった中から100個取 り出して計算しようというのはおかしなことです。最初から100個を調べて要因Aによる不良品の信頼区間を調べようという計画を立てたら，100個たまっ たときにすぐに調査と計算をすればよかったのです。漫然と500個たまるまで待って，その中から100個を取り出すのは，残り400個をとるために使った 時間と計算に使われなかった400個のデータが無駄になるのです。時間を無駄にしたくないなら，そのときまでに得られた全データ（500個）を使えばよい だけです。精度も高くなりますし。

No.11060　Re: 二項分布におけるp値の範囲推定　　【伊藤】　2009/10/14(Wed) 10:56

青木先生　丁寧なご回答ありがとうございました。
前段の内容で私の疑問は解決いたしました。

最終段のアドバイスに対しまして，若干の補足をさせていただきます。

実際の解析は次の様に行っています。
（1）あるロットについて全数検査を行い不良品をすべてカウントします（例では500個）。この検出は比較的簡便な方法を用いるので短時間に終了します。
（2）不良品のうちいくつかをサンプリングして不良品の要因解析を行います（例では100個）。この解析は（1）の方法と異なり時間と労力が掛かるので長時間必要です。
今，要因Aで不良となっている不良品がすべての不良品の中にどれくらいの割合で入っているか推定したいと考えております。ロットすべての中の要因Aの不良割合を知りたいわけではないので無限母集団とは考えておりません。

不 良品すべての要因解析を行うのは，時間とコストの関係でなかなか難しく，求める信頼区間の大きさとの兼ね合いと考えております。500個すべて不良解析し たとき，私の計算での±0.026では，全数不良解析のメリットがあまりないように思っておりまして悩んでおりました。

本問題では製造条件をいろいろ変えて解析していますので(1)で簡易的でありますが全数検査を行っています。将来，元のロットからの抜き取り検査で対応できないかを考えるときに先生のアドバイスを生かしたいと思っています。どうもありがとうございました。

● 「統計学関連なんでもあり」の過去ログ--- 043 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る